Opisana, upisana i spolja pripisana kružnica

Opisana kružnica oko mnogougla je kružnica koja prolazi kroz sva temena mnogougla. Centar ove kružnice se nalazi u preseku simetrala stranica i njen poluprečnik je rastojanje centra od bilo kog temena mnogougla. Mnogougao oko koga se može opisati krug naziva se tetivni mnogougao. Svi pravilni mnogouglovi su tetivni.
Kružnica koja dodiruje sve stranice jednog mnogougla naziva se upisana kružnica tog mnogougla. Centar ove kružnice se nalazi u preseku simetrala uglova i njen poluprečnik je rastojanje centra od bilo koje stranice mnogougla. U svaki pravilni mnogougao može da se upiše kružnica.
Centar spolja pripisane kružnice pravilnog mnogougla dobijamo u preseku simetrale jednog unutrašnjeg ugla i simetrale spoljašnjih uglova kod druga dva susedna temena. Poluprečnik je rastojanje centra od stranice mnogougla koju kružnica dodiruje.

Trougao

Oko svakog trougla može da se opiše kružnica. Centar opisane kružnice je presek simetrala stranica trougla.

Teorema 1. (O centru opisanog kruga) Simetrale stranica trougla seku se u jednoj tački.^{[1]‍:str. 60}
Dokaz: Neka je S zajednička tačka simetrale ${\displaystyle s}$₁-stranice ${\displaystyle BC}$ i simetrale ${\displaystyle s}$₂-stranice ${\displaystyle AC}$ trougla ∆${\displaystyle ABC}$. Pošto ${\displaystyle S}$ pripada simetrali ${\displaystyle s}$₁, imamo da je ${\displaystyle BS}$≅${\displaystyle CS}$, a pošto ${\displaystyle S}$ pripada simetrali ${\displaystyle s}$₂, imamo da je ${\displaystyle AS}$≅${\displaystyle CS}$. Odatle sledi da je ${\displaystyle AS}$≃${\displaystyle BS}$≅${\displaystyle CS}$, tj da ${\displaystyle S}$ pripada i simetrali ${\displaystyle s}$₃, pa je ${\displaystyle S}$ presek svih simetrala. Kružnica sa centrom ${\displaystyle S}$ i poluprečnikom ${\displaystyle AS}$ sadrži sva temena trougla, pa je to opisana kružnica oko trougla ∆${\displaystyle ABC}$.

Jednakostraničan trougao

Kod jednakostraničnog trougla poluprečnik opisane kružnice iznosi ${\displaystyle {\frac {2}{3}}}$ visine: ${\displaystyle r}$_o=${\displaystyle {\frac {2}{3}}h}$ ili ${\displaystyle r}$₀=${\displaystyle {\frac {a{\sqrt {3}}}{3}}}$.

Površina opisanog kruga je: ${\displaystyle P=r_{0}^{2}\pi }$.

Jednakokraki trougao

Kod jednakokrakog trougla centar opisane kružnice je na sredini visine, ${\displaystyle r={\frac {h_{a}}{2}}}$, gde je ${\displaystyle h_{a}={\sqrt {b^{2}-({\frac {a}{2}})^{2}}}}$.

Površina tog kruga je: ${\displaystyle P=({\frac {h_{a}}{2}})^{2}\pi }$.

Pravougli trougao

Tvrđenje 1.: Centar opisane kružnice pravouglog trougla je središte hipotenuze.

Dokaz: Neka je ${\displaystyle O}$ središte hipotenuze. Neka je ${\displaystyle P}$ središte ${\displaystyle AB}$. Tada je ${\displaystyle OP}$ srednja linija trougla ∆${\displaystyle ABC}$ i ${\displaystyle OP}$ je paralelna sa ${\displaystyle BC}$ pa je ${\displaystyle AB}$ normalno na ${\displaystyle OP}$. Tada iz podudarnosti trouglova ∆${\displaystyle AOP}$ i ∆${\displaystyle BOP}$ sledi da je ${\displaystyle OB}$≅${\displaystyle OA}$. Pošto je i ${\displaystyle OA}$≅${\displaystyle OC}$ sledi da je ${\displaystyle O}$ centar opisane kružnice, a poluprečnik je pola hipotenuze.

Površina tog kruga je ${\displaystyle P=({\frac {c}{2}})^{2}\pi }$

Položaj centra u odnosu na trougao

Oštrougli	Tupougli	Pravougli
centar unutar trougla	centar izvan trougla	centar na sredini hipotenuze

U svaki trougao može da se upiše kružnica. Centar te kružnice se nalazi u preseku simetrala uglova.

Teorema 2. (O centru upisane kružnice) Simetrale uglova trougla se seku u jednoj tački^{[1]‍:str. 61}

Dokaz: Neka je ${\displaystyle O}$ presek simetrale uglova ∠${\displaystyle CAB}$ i ∠${\displaystyle ABC}$. Neka su ${\displaystyle OM}$, ${\displaystyle ON}$ i ${\displaystyle OP}$ normale iz ${\displaystyle O}$ na stranice ${\displaystyle AB}$, ${\displaystyle BC}$ i ${\displaystyle AC}$. Iz podudarnosti trouglova ∆${\displaystyle BMO}$ i ∆${\displaystyle BNO}$ sledi da je ${\displaystyle OM}$≅${\displaystyle ON}$. Iz ${\displaystyle OP}$≅${\displaystyle OM}$ i ${\displaystyle OM}$≅${\displaystyle ON}$ sledi da je ${\displaystyle OP}$≅${\displaystyle ON}$ iz čega sledi podudarnost trouglova ∆${\displaystyle CNO}$ i ∆${\displaystyle CPO}$ odakle sledi ∠${\displaystyle BCO}$≅∠${\displaystyle ACO}$ i ${\displaystyle O}$ pripada preseku svih simetrala i ${\displaystyle O}$ je centar opisane kružnice.

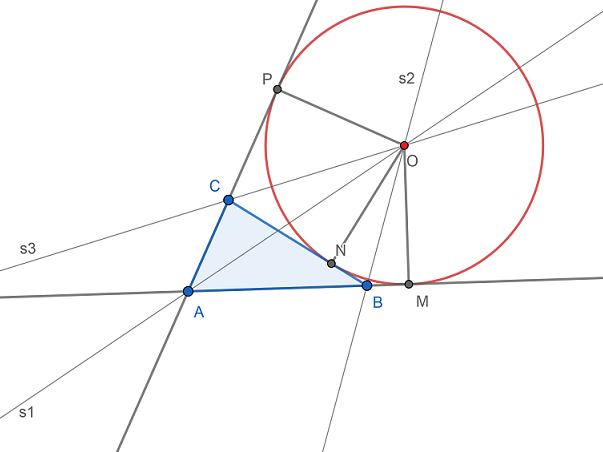
Teorema 3.: Simetrala jednog unutrašnjeg ugla trougla i simetrala spoljašnjih uglova kod druga dva temena seku se u jednoj tački-centru spolja pripisane kružnice.

Četvorougao

Tangentni četvorougao

Četvorougao čije su ivice tangente jednog kruga, tj. četvorougao u koji se može upisati krug, naziva se tangentni četvorougao.

Za dokazivanje tog kriterijuma koristi se teorema o podudarnosti tangentnih duži, tj. odsečaka tangente na dati krug od tačke iz koje je ona konstruisana do tačke dodira.

Teorema 1. Tangentne duži konstruisane iz iste tačke van datog kruga su međusobno podudarne.^{[1]‍:str. 101}

Teorema 2. Četvorougao ${\displaystyle ABCD}$ je tangentni ako i samo ako je ${\displaystyle AB+CD=BC+AD}$.^{[1]‍:str. 101–2}

Dokaz:
(⇒) Pretpostavimo da je četvorougao ${\displaystyle ABCD}$ tangentni. Neka su ${\displaystyle P,Q,R,S}$ dodirne tačke ivica ${\displaystyle AB,BC,CD,DA}$ sa upisanim krugom ${\displaystyle k}$. Kako su tangentne duži podudarne, to je ${\displaystyle AP}$≅${\displaystyle AS}$; ${\displaystyle BP}$≅${\displaystyle BQ}$; ${\displaystyle CQ}$≅${\displaystyle CR}$; ${\displaystyle DR}$≅${\displaystyle DS}$. Na osnovu toga je: ${\displaystyle AP+PB+CR+RD=AS+SD+BQ+QC}$, tj. ${\displaystyle AB+CD=AD+BC}$.

(⇐) Neka su u četvorouglu ${\displaystyle ABCD}$ zbirovi naspramnih ivica jednaki. Postoji krug ${\displaystyle k}$ koji dodiruje ivice ${\displaystyle AB,BC}$ i ${\displaystyle DA}$ tog četvorougla (njegov centar je presek simetrala unutrašnjih uglova kod temena ${\displaystyle A}$ i ${\displaystyle B}$ četvorougla). Neka je ${\displaystyle D'}$ presek druge tangente iz tačke ${\displaystyle C}$ kruga ${\displaystyle k}$ i prave ${\displaystyle AD}$. Pretpostavimo da je ${\displaystyle D'}$≠${\displaystyle D}$. Prema već dokazanom delu teoreme važi ${\displaystyle AB+CD=BC+D'A}$, pa kako je po pretpostavci ${\displaystyle AB+CD=BC+DA}$, to je ${\displaystyle CD'-CD=D'A-DA}$, tj. ${\displaystyle CD'=D'A-DA+CD}$.

Ako je tačka ${\displaystyle D}$ između tačaka ${\displaystyle D'}$ i ${\displaystyle A}$ ova relacija postaje ${\displaystyle CD'=CD+DD'}$, a to je nemoguće na osnovu nejednakosti trougla. Na sličan način dolazimo do kontradikcije i u slučaju kada ${\displaystyle D}$ nije između tačaka ${\displaystyle D'}$ i ${\displaystyle A}$. Dakle, ${\displaystyle D'=D}$, tj. krug ${\displaystyle k}$ dodiruje i četvrtu ivicu četvorougla ${\displaystyle ABCD}$.

Neposredna posledica ove teoreme je da se u kvadrat, romb i deltoid mogu upisati krugovi.

Tetivni četvorougao

Četvorougao oko koga se može opisati krug, tj. čije su sve ivice tetive nekog kruga naziva se tetivni četvorougao. Kao što postoji kriterijum za utvrđivanje da li je četvorougao tangentni, postoji i važna teorema koja daje neophodan i dovoljan uslov da četvorougao bude tetivni.

Teorema 1. Konveksni četvorougao je tetivni ako i samo ako su njegovi naspramni uglovi suplementni.^{[1]‍:str. 103}

Dokaz:

(⇒) Pretpostavimo najpre da je četvorougao ${\displaystyle ABCD}$ tetivni. Kako je četvorougao konveksan, temena ${\displaystyle A}$ i ${\displaystyle C}$ su sa raznih strana prave određene dijagonalom ${\displaystyle BD}$. Na osnovu posledice (Periferijski uglovi kruga nad istom tetivom, čija su temena sa raznih strana prave određene tom tetivom, su suplementni), uglovi ∠${\displaystyle BAD}$ i ∠${\displaystyle BCD}$ četvorougla su suplementni.
(⇐) Pretpostavimo sada da su naspramni uglovi četvorougla ${\displaystyle ABCD}$ suplementni. Neka je ${\displaystyle k}$ krug opisan oko trougla ∆${\displaystyle ABD}$. Tada se iz četvrtog temena ${\displaystyle C}$ tetiva ${\displaystyle BD}$ vidi pod uglom koji je suplementan uglu kod temena ${\displaystyle A}$, pa tačka ${\displaystyle C}$ pripada krugu.

Teorema 2. Ako je ${\displaystyle ABCD}$ konveksan četvorougao i ∠${\displaystyle ACB}$≅∠${\displaystyle ADB}$ tada je on tetivni četvorougao.

Reference

Literatura