Patrulater inscriptibil

În geometria euclidiană un patrulater inscriptibil^[1][2][3] sau patrulater înscris^[4] este un patrulater ale cărui vârfuri se află toate pe un singur cerc.^[4] Acest cerc se numește cerc circumscris. De obicei se presupune că patrulaterul este convex, dar există și patrulatere inscriptibile autointersectate. Formulele și proprietățile prezentate mai jos sunt valabile în cazul convex.

Toate triunghiurile au un cerc circumscris, dar nu toate patrulaterele au unul. Un exemplu de patrulater care nu este inscriptibil este un romb care nu este și pătrat.

Cazuri particulare

Orice pătrat, dreptunghi, trapez isoscel sau antiparalelogram este inscriptibil. Un romboid este inscriptibil dacă și numai dacă are două unghiuri drepte. Un Patrulater bicentric este un patrulater inscriptibil, fiind atât circumscriptibil, cât și exscriptibil. Un patrulater armonic este un patrulater inscriptibil în care produsele lungimilor laturilor opuse sunt egale.

Caracteristici

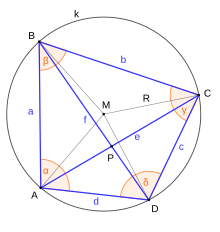
Centrul cercului circumscris

Un patrulater convex este inscriptibil dacă și numai dacă cele patru mediatoare ale laturilor sunt concurente. Acest punct comun este centrul cercului circumscris.^[5]

Unghiuri suplementare

Un patrulater convex ABCD este inscriptibil dacă și numai dacă unghiurile sale opuse sunt suplementare, adică^[5][6]

${\displaystyle \alpha +\gamma =\beta +\delta =\pi \ {\text{radiani}}\ (=180^{\circ }).}$

Teorema directă a fost Propoziția 22 din Cartea a 3-a din Elementele lui Euclid.^[7] Echivalent, un patrulater convex este inscriptibil dacă și numai dacă fiecare unghi exterior este egal cu unghiul interior opus.

În 1836 Duncan Gregory a generalizat acest rezultat după cum urmează: pentru orice 2n-gon inscriptibil convex, cele două sume ale unghiurilor interioare alternate sunt fiecare egală cu (n − 1)π.^[8] Considerînd proiecția stereografică (tangenta jumătății de unghi) a fiecărui unghi, aceasta poate fi exprimat ca

${\displaystyle {\frac {\tan {\frac {\alpha }{2}}+\tan {\frac {\gamma }{2}}}{1-\tan {\frac {\alpha }{2}}\tan {\frac {\gamma }{2}}}}={\frac {\tan {\frac {\beta }{2}}+\tan {\frac {\delta }{2}}}{1-\tan {\frac {\beta }{2}}\tan {\frac {\delta }{2}}}}=\infty .}$

Ceea ce implică^[9]

${\displaystyle \tan {\frac {\alpha }{2}}\tan {\frac {\gamma }{2}}=\tan {\frac {\beta }{2}}{\tan {\frac {\delta }{2}}}=1}$

Unghiuri dintre laturi și diagonale

Un patrulater convex ABCD este inscriptibil dacă și numai dacă un unghi dintre o latură și o diagonală este egal cu unghiul dintre latura opusă și cealaltă diagonală.^[10] Adică, de exemplu,

${\displaystyle \angle ACB=\angle ADB.}$

Intersecția diagonalelor

Dacă două drepte, una care conține segmentul AC și cealaltă care conține segmentul BD, se intersectează în P, atunci cele patru puncte A, B, C, D sunt pe acelați cerc dacă și numai dacă^[11]

${\displaystyle AP\cdot PC=BP\cdot PD.}$

Intersecția P poate fi internă sau externă cercului. În primul caz, patrulaterul inscriptibil este ABCD, iar în al doilea caz patrulaterul inscriptibil este ABDC. Când intersecția este internă, egalitatea afirmă că produsul lungimii segmentelor în care P împarte o diagonală este egal cu cel al celeilalte diagonale. Aceasta este cunoscută sub denumirea de teorema coardelor concurente, deoarece diagonalele patrulaterului inscriptibil sunt coarde ale cercului circumscris.

Teorema Ptolemeu

Teorema lui Ptolemeu exprimă produsul lungimilor celor două diagonale e și f ale unui patrulater inscriptibil ca sumă a produselor laturilor opuse:^[12]:p.25[6]

${\displaystyle ef=ac+bd,}$

unde a, b, c, d sunt lungimile laturilor, în ordine. Inversa acestei teoreme este și ea adevărată. Adică, dacă această ecuație este îndeplinită într-un patrulater convex, atunci patrulaterul este inscriptibil.

Aria

Aria K a unui patrulater inscriptibil cu laturile a, b, c, d este dată de formula lui Brahmagupta^[12]:p.24

${\displaystyle K={\sqrt {(s-a)(s-b)(s-c)(s-d)}}}$

unde s este semiperimetrul: ${\displaystyle s={\frac {1}{2}}(a+b+c+d)}$. Acesta este un corolar al formulei lui Bretschneider pentru patrulaterul general, deoarece în cazul patrulaterului inscriptibil unghiurile opuse sunt suplementare. Iar dacă d = 0, patrulaterul inscriptibil devine un triunghi iar formula se reduce la formula lui Heron.

Aria unui patrulater inscriptibil având unghiul B între laturile a și b se poate calcula cu^[12]:p.25

${\displaystyle K={\frac {1}{2}}(ab+cd)\sin {B}.}$

Diagonale

Într-un patrulater inscriptibil lungimea diagonalelor e și f se poate exprima în funcție de lungimile laturilor^{[12]:p.25,[13][14]:p. 84}

${\displaystyle e={\sqrt {\frac {(ac+bd)(ad+bc)}{ab+cd}}}}$   și   ${\displaystyle f={\sqrt {\frac {(ac+bd)(ab+cd)}{ad+bc}}}}$

ceea ce duce la teorema lui Ptolemeu (${\displaystyle pq=ac+bd.}$.)

Conform celei a doua teoreme a lui Ptolemeu,^{[12]:p.25,[13]}

${\displaystyle {\frac {p}{q}}={\frac {ad+bc}{ab+cd}}.}$

Formule pentru unghiuri

Pentru un patrulater inscriptibil având unghiul A între laturile a și d, valorile funcțiilor trigonometrice pentru A se obțin din^[15]

${\displaystyle \cos A={\frac {a^{2}+d^{2}-b^{2}-c^{2}}{2(ad+bc)}},}$

${\displaystyle \sin A={\frac {2{\sqrt {(s-a)(s-b)(s-c)(s-d)}}}{(ad+bc)}},}$

${\displaystyle \tan {\frac {A}{2}}={\sqrt {\frac {(s-a)(s-d)}{(s-b)(s-c)}}}.}$

Unghiul θ dintre diagonale satisface relația^[12]:p.26

${\displaystyle \tan {\frac {\theta }{2}}={\sqrt {\frac {(s-b)(s-d)}{(s-a)(s-c)}}}.}$

Anticentrul

Se poate demonstra că, într-un patrulater inscriptibil, perpendicularele duse prin mijlocul fiecarei laturi la latura opusă sunt concurente, punctul de concurență fiind cunoscut ca anticentrul patrulaterului sau punctul lui Mathot.^[16]

Mai întâi se va demonstra următoarea propoziție:

Teorema 1. Dacă ${\displaystyle O_{1},O_{2},O_{3},O_{4}}$ sunt centrele cercurilor circumscrise triunghiurilor AEB, BEC, CED și respectiv DEA, atunci:

(a) Patrulaterul ${\displaystyle O_{1}O_{2}O_{3}O_{4}}$ este paralelogram.

(b) Dacă ${\displaystyle \Gamma }$ este punctul de intersecție a diagonalelor paralelogramului ${\displaystyle O_{1}O_{2}O_{3}O_{4}}$, atunci punctele O, Γ, E sunt coliniare, punctul Γ fiind mijlocul segmentului ${\displaystyle [OE]}$.

Demonstrație.

(a) Deoarece ${\displaystyle O_{1}O_{4}}$ este mediatoarea segmentului ${\displaystyle [AE]}$, iar ${\displaystyle O_{2}O_{3}}$ este mediatoarea segmentului ${\displaystyle [EC]}$, rezultă că ${\displaystyle O_{1}O_{4}\perp AC,\;O_{2}O-3\perp AC}$, deci ${\displaystyle O_{1}O_{4}\parallel O_{2}O_{3}}$. La fel se demonstrează că ${\displaystyle O_{1}O_{2}\parallel O_{3}O_{4}}$. Deci ${\displaystyle O_{1}O_{2}O_{3}O_{4}}$ este paralelogram.

(b) Se notează cu F piciorul perpendicularei din E pe AB. Din ${\displaystyle m({\widehat {FEA}})=90^{o}-m({\widehat {BAE}}),\;m({\widehat {CEO_{3}}})=90^{o}-m({\widehat {CDE}}),\;{\widehat {BAE}}\equiv {\widehat {CDE}}\;}$ rezultă că ${\displaystyle {\widehat {FEA}}\equiv {\widehat {CEO_{3}}}}$. Așadar, ${\displaystyle F,E,O_{3}}$ sunt coliniare, deci ${\displaystyle EO_{3}\perp AB}$, deci ${\displaystyle O_{3}E\parallel OO_{1}}$; analog se demonstrează ${\displaystyle O_{1}E\parallel OO_{3},\;O_{4}E\parallel OO_{2},\;O_{2}E\parallel OO_{4}}$, de unde rezultă că patrulaterele ${\displaystyle O_{1}EO_{3}O,\;O_{2}EO_{4}O}$ sunt paralelograme. Deci Γ fiind mijlocul segmentului ${\displaystyle [OE]}$.

Acum se va demonstra următoarea teoremă:

Teorema 2. Se consideră patrulaterul inscriptibil ${\displaystyle ABCD}$, înscris în cercul de centru ${\displaystyle O}$ și fie ${\displaystyle E}$ intersecția diagonalelor ${\displaystyle AC}$ și ${\displaystyle BD}$ și ${\displaystyle H_{1},H_{2},H_{3},H_{4}}$ ortocentrele triunghiurilor ${\displaystyle AEB,BEC,CED}$ și respectiv ${\displaystyle DEA}$. Atunci:

(a) Patrulaterul ${\displaystyle H_{1}H_{2}H_{3}H_{4}}$ este paralelogram;

(b) Intersecția diagonalelor paralelogramului ${\displaystyle H_{1}H_{2}H_{3}H_{4}}$ este chiar punctul Mathot al patrulaterului ${\displaystyle ABCD}$.

Demonstrație.

(a) ${\displaystyle {\vec {OA}}={\vec {OO_{4}}}+{\vec {O_{4}A}}={\vec {OO_{1}}}+{\vec {O_{1}A}}}$ și alte trei relații similare pentru ${\displaystyle {\vec {OB}},{\vec {OC}},{\vec {OD}}}$. Prin însumarea acestor patru relații se obține:

${\displaystyle 2({\vec {OA}}+{\vec {OB}}+{\vec {OC}}+{\vec {OD}})=2({\vec {OO_{1}}}+{\vec {OO_{2}}}+{\vec {OO_{3}}}+{\vec {OO_{4}}})+({\vec {O_{1}A}}+{\vec {O_{1}B}}+{\vec {O_{1}E}})+}$

${\displaystyle +({\vec {O_{2}B}}+{\vec {O_{2}C}}+{\vec {O_{2}E}})+({\vec {O_{3}C}}+{\vec {O_{3}D}}+{\vec {O_{3}E}})+({\vec {O_{4}D}}+{\vec {O_{4}A}}+{\vec {O_{4}E}})+({\vec {EO_{1}}}+{\vec {EO_{2}}}+{\vec {EO_{3}}}+{\vec {EO_{4}}}).}$

În continuare se aplică relația Sylvester. Rezultă în continuare:

${\displaystyle 2({\vec {OA}}+{\vec {OB}}+{\vec {OC}}+{\vec {OD}})=2({\vec {OO_{1}}}+{\vec {OO_{2}}}+{\vec {OO_{3}}}+{\vec {OO_{4}}})+{\vec {O_{1}H_{1}}}+{\vec {O_{2}H_{2}}}+{\vec {O_{3}H_{3}}}+{\vec {O_{4}H_{4}}}+{\vec {EO_{1}}}+{\vec {EO_{2}}}+{\vec {EO_{3}}}+{\vec {EO_{4}}}}$.

Se va ține cont că ${\displaystyle {\vec {OO_{1}}}+{\vec {O_{1}H_{1}}}={\vec {OH_{1}}}}$ și celelalte trei similare.

În continuare, se va ține cont că, deoarece ${\displaystyle O_{1}O_{2}O_{3}O_{4}}$ este paralelogram, ${\displaystyle \Gamma }$ fiind intersecția diagonalelor, pentru orice punct ${\displaystyle M}$ din spațiu:

${\displaystyle (1)\;\;4{\vec {M\Gamma }}={\vec {MO_{1}}}+{\vec {MO_{2}}}+{\vec {MO_{3}}}+{\vec {MO_{4}}},}$

Deci:

${\displaystyle {\vec {OO_{1}}}+{\vec {OO_{2}}}+{\vec {OO_{3}}}+{\vec {OO_{4}}}=4{\vec {O\Gamma }}}$.

Deoarece ${\displaystyle \Gamma }$ este mijlocul segmentului ${\displaystyle [OE]}$, rezultă: ${\displaystyle {\vec {O\Gamma }}+{\vec {E\Gamma }}={\vec {0}}}$. Se notează ${\displaystyle \Omega '}$ intersecția diagonalelor paralelogramului ${\displaystyle H_{1}H_{2}H_{3}H_{4}}$. Aplicând formula (1), se va obține:

${\displaystyle {\vec {OH_{1}}}+{\vec {OH_{2}}}+{\vec {OH_{3}}}+{\vec {OH_{4}}}=4{\vec {O\Omega '}}}$.

Așadar, ${\displaystyle 2({\vec {OA}}+{\vec {OB}}+{\vec {OC}}+{\vec {OD}})=4{\vec {O\Omega '}}}$.

Mai departe se va ține cont că, deoarece ${\displaystyle \Omega }$ este punctul Mathot al patrulaterului inscriptibil ${\displaystyle ABCD}$, există relația:

${\displaystyle {\vec {OA}}+{\vec {OB}}+{\vec {OC}}+{\vec {OD}}=2{\vec {O\Omega }}}$

Va rezulta că ${\displaystyle 4{\vec {O\Omega }}=4{\vec {O\Omega '}}}$, deci ${\displaystyle \Omega }$ coincide cu ${\displaystyle \Omega '}$ și astfel teorema este demonstrată.

Observație. Din relația (1) se poate deduce:

${\displaystyle {\vec {O_{1}H_{1}}}+{\vec {O_{2}H_{2}}}+{\vec {O_{3}H_{3}}}+{\vec {O_{4}H_{4}}}=4{\vec {\Gamma \Omega }}}$.

Note

Lectură suplimentară

• en D. Fraivert: Pascal-points quadrilaterals inscribed in a cyclic quadrilateral

legături externe

• en Derivation of Formula for the Area of Cyclic Quadrilateral
• en Incenters in Cyclic Quadrilateral la cut-the-knot
• en Four Concurrent Lines in a Cyclic Quadrilateral la cut-the-knot
• en Eric W. Weisstein, Cyclic quadrilateral la MathWorld.