Estrutura causal

Na física matemática, a estrutura causal de uma variedade Lorentziana [en] descreve as relações causais [en] entre pontos na variedade.

Introdução

Na física moderna (especialmente na relatividade geral), o espaço-tempo é representado por uma variedade Lorentziana [en]. As relações causais entre pontos na variedade são interpretadas como descrevendo quais eventos no espaço-tempo podem influenciar quais outros eventos.

A estrutura causal de uma variedade lorentziana arbitrária (possivelmente curva) torna-se mais complicada pela presença de curvatura. As discussões sobre a estrutura causal de tais variedades devem ser formuladas em termos de curvas suaves que unem pares de pontos. As condições nos vetores tangentes das curvas definem então as relações causais.

Vetores tangentes

Se ${\displaystyle \,(M,g)}$ é uma variedade Lorentziana (para a métrica ${\displaystyle g}$ na variedade ${\displaystyle M}$) então os vetores tangentes diferentes de zero em cada ponto na variedade podem ser classificados em três tipos disjuntos. Um vetor tangente ${\displaystyle X}$ é:

• semelhante ao tempo se ${\displaystyle \,g(X,X)<0}$
• nulo ou semelhante a luz se ${\displaystyle \,g(X,X)=0}$
• semelhante ao espaço se ${\displaystyle \,g(X,X)>0}$

Aqui usamos a assinatura métrica ${\displaystyle (-,+,+,+,\cdots )}$. Dizemos que um vetor tangente não é semelhante ao espaço se for nulo (semelhante a luz) ou semelhante ao tempo.

A variedade Lorentziana canônica é o espaço-tempo de Minkowski, onde ${\displaystyle M=\mathbb {R} ^{4}}$ e ${\displaystyle g}$ é a métrica de Minkowski [en] plana [en]. Os nomes dos vetores tangentes vêm da física desse modelo. As relações causais entre pontos no espaço-tempo de Minkowski assumem uma forma particularmente simples porque o espaço tangente também é ${\displaystyle \mathbb {R} ^{4}}$ e, portanto, os vetores tangentes podem ser identificados com pontos no espaço. O vetor quadridimensional ${\displaystyle X=(t,r)}$ é classificado de acordo com o sinal de ${\displaystyle g(X,X)=-c^{2}t^{2}+\|r\|^{2}}$, onde ${\displaystyle r\in \mathbb {R} ^{3}}$ é uma coordenada cartesiana no espaço tridimensional, ${\displaystyle c}$ é a constante que representa o limite de velocidade universal e ${\displaystyle t}$ é o tempo. A classificação de qualquer vetor no espaço será a mesma em todos os referenciais relacionados por uma transformação de Lorentz (mas não por uma transformação de Poincaré geral porque a origem pode ser deslocada) por causa da invariância da métrica.

Orientabilidade temporal

Em cada ponto em ${\displaystyle M}$, os vetores tangentes semelhantes ao tempo no espaço tangente do ponto podem ser divididos em duas classes. Para fazer isso, primeiro definimos uma relação de equivalência em pares de vetores tangentes semelhantes ao tempo.

Se ${\displaystyle X}$ e ${\displaystyle Y}$ são dois vetores tangentes semelhantes ao tempo em um ponto, dizemos que ${\displaystyle X}$ e ${\displaystyle Y}$ são equivalentes (escrito ${\displaystyle X\sim Y}$) se ${\displaystyle \,g(X,Y)<0}$.

Existem então duas classes de equivalência que entre elas contêm todos os vetores tangentes do tipo tempo no ponto. Podemos (arbitrariamente) chamar uma dessas classes de equivalência dirigida ao futuro e chamar a outra de dirigida ao passado. Fisicamente, essa designação das duas classes de vetores temporais direcionados ao futuro e ao passado corresponde a uma escolha de uma seta de tempo no ponto. As designações dirigidas ao futuro e ao passado podem ser estendidas para vetores nulos em um ponto por continuidade.

Uma variedade Lorentziana [en] é orientável no tempo^[1] se uma designação contínua de direção ao futuro e direção ao passado para vetores não-espaciais puder ser feita em toda a variedade.

Curvas

Um caminho em ${\displaystyle M}$ é um mapa contínuo [en] ${\displaystyle \mu :\Sigma \to M}$ onde ${\displaystyle \Sigma }$ é um intervalo que não é degenerado (ou seja, um conjunto conectado contendo mais de um ponto) em ${\displaystyle \mathbb {R} }$. Um caminho suave tem ${\displaystyle \mu }$ diferenciável um número apropriado de vezes (normalmente ${\displaystyle C^{\infty }}$) e um caminho regular tem derivada que não é nula.

Uma curva em ${\displaystyle M}$ é a imagem de um caminho ou, mais propriamente, uma classe de equivalência de imagens de caminho relacionada por reparametrização, ou seja, homeomorfismos ou difeomorfismos de ${\displaystyle \Sigma }$. Quando ${\displaystyle M}$ é orientável no tempo, a curva é orientada se for necessário que a alteração do parâmetro seja monotônica.

Curvas regulares suaves (ou caminhos) em ${\displaystyle M}$ podem ser classificadas dependendo de seus vetores tangentes. Tal curva é

• cronológica (ou semelhante ao tempo) se o vetor tangente for semelhante ao tempo em todos os pontos da curva. Também chamada de linha mundial.^[2]
• nula (semelhante à luz) se o vetor tangente for nulo (semelhante à luz) em todos os pontos da curva.
• semelhante ao espaço se o vetor tangente for semelhante ao espaço em todos os pontos da curva.
• causal (ou que não é semelhante ao espaço) se o vetor tangente for semelhante ao tempo ou nulo (semelhante à luz) em todos os pontos da curva.

Os requisitos de regularidade e não degenerescência de ${\displaystyle \Sigma }$ garantem que curvas causais fechadas (como aquelas que consistem em um único ponto) não sejam automaticamente admitidas por todos os espaços-tempos.

Se a variedade é orientável no tempo, então as curvas que não são semelhantes ao tempo podem ainda ser classificadas dependendo de sua orientação em relação ao tempo.

Uma curva cronológica, nula (semelhante à luz) ou causal, em ${\displaystyle M}$ é

• orientada ao futuro se, para cada ponto na curva, o vetor tangente for direcionado ao futuro.
• direcionada ao passado se, para cada ponto na curva, o vetor tangente é direcionado ao passado.

Essas definições aplicam-se apenas às curvas causais (cronológicas ou nulas), porque apenas vetores tangentes semelhantes ao tempo ou nulos (semelhante à luz) podem receber uma orientação em relação ao tempo.

• Uma curva semelhante ao tempo fechada é uma curva fechada que é semelhante ao tempo direcionada ao futuro (ou semelhante ao tempo direcionada ao passado) em todos os lugares.
• Uma curva nula (semelhante à luz) fechada é uma curva fechada que é nula (semelhante à luz) em toda parte direcionada ao futuro (ou nula (semelhante à luz) em toda parte direcionada ao passado).

A holonomia da razão da taxa de mudança do parâmetro afim em torno de uma geodésica nula (semelhante à luz) fechada é o fator de desvio para o vermelho.

Relações causais

Existem várias relações [en] causais entre os pontos ${\displaystyle x}$ e ${\displaystyle y}$ na variedade ${\displaystyle M}$.

• ${\displaystyle x}$ precede cronologicamente ${\displaystyle y}$ (muitas vezes denotado ${\displaystyle \,x\ll y}$) se existe uma curva cronológica (semelhante ao tempo) dirigida ao futuro de ${\displaystyle x}$ para ${\displaystyle y}$.
• ${\displaystyle x}$ estritamente precede causalmente ${\displaystyle y}$ (muitas vezes denotado ${\displaystyle x<y}$) se existe uma curva causal (que não é semelhante ao espaço) direcionada ao futuro de ${\displaystyle x}$ para ${\displaystyle y}$.
• ${\displaystyle x}$ causalmente precede ${\displaystyle y}$ (muitas vezes denotado ${\displaystyle x\prec y}$ ou ${\displaystyle x\leq y}$) se ${\displaystyle x}$ precede estritamente causalmente ${\displaystyle y}$ ou ${\displaystyle x=y}$.
• ${\displaystyle x}$ horismos ${\displaystyle y}$^[3] (muitas vezes denotado ${\displaystyle x\to y}$ ou ${\displaystyle x\nearrow y}$) se ${\displaystyle x=y}$ ou existe uma curva nula direcionada ao futuro de ${\displaystyle x}$ para ${\displaystyle y}$^[4] (ou equivalentemente, ${\displaystyle x\prec y}$ e ${\displaystyle x\not \ll y}$).

Essas relações satisfazem as seguintes propriedades:

• ${\displaystyle x\ll y}$ implica ${\displaystyle x\prec y}$ (isso decorre trivialmente da definição)^[5]
• ${\displaystyle x\ll y}$, ${\displaystyle y\prec z}$ implica ${\displaystyle x\ll z}$^[5]
• ${\displaystyle x\prec y}$, ${\displaystyle y\ll z}$ implica ${\displaystyle x\ll z}$^[5]
• ${\displaystyle \ll }$, ${\displaystyle <}$, ${\displaystyle \prec }$ são transitivas.^[5] ${\displaystyle \to }$ não é transitiva.^[6]
• ${\displaystyle \prec }$, ${\displaystyle \to }$ são reflexivas^[4]

Para um ponto ${\displaystyle x}$ na variedade ${\displaystyle M}$ definimos^[5]

• O futuro cronológico de ${\displaystyle x}$, denotado ${\displaystyle \,I^{+}(x)}$, como o conjunto de todos os pontos ${\displaystyle y}$ em ${\displaystyle M}$ tal que ${\displaystyle x}$ cronologicamente precede ${\displaystyle y}$:

${\displaystyle \,I^{+}(x)=\{y\in M|x\ll y\}}$

• O passado cronológico de ${\displaystyle x}$, denotado ${\displaystyle \,I^{-}(x)}$, como o conjunto de todos os pontos ${\displaystyle y}$ em ${\displaystyle M}$ tal que ${\displaystyle y}$ cronologicamente precede ${\displaystyle x}$:

${\displaystyle \,I^{-}(x)=\{y\in M|y\ll x\}}$

Nós definimos similarmente

• O futuro causal (também chamado de futuro absoluto) de ${\displaystyle x}$, denotado ${\displaystyle \,J^{+}(x)}$, como o conjunto de todos os pontos ${\displaystyle y}$ em ${\displaystyle M}$ tal que ${\displaystyle x}$ preceda causalmente ${\displaystyle y}$:

${\displaystyle \,J^{+}(x)=\{y\in M|x\prec y\}}$

• O passado causal (também chamado de passado absoluto) de ${\displaystyle x}$, denotado ${\displaystyle \,J^{-}(x)}$, como o conjunto de todos os pontos ${\displaystyle y}$ em ${\displaystyle M}$ tal que ${\displaystyle y}$ preceda causalmente ${\displaystyle x}$:

${\displaystyle \,J^{-}(x)=\{y\in M|y\prec x\}}$

• O cone nulo futuro de ${\displaystyle x}$ como o conjunto de todos os pontos ${\displaystyle y}$ em ${\displaystyle M}$ tal que ${\displaystyle x\to y}$.
• O cone nulo passado de ${\displaystyle x}$ como o conjunto de todos os pontos ${\displaystyle y}$ em ${\displaystyle M}$ tal que ${\displaystyle y\to x}$.
• O cone de luz de ${\displaystyle x}$ como os cones nulos futuros e passados de ${\displaystyle x}$ juntos.^[7]
• em outro lugar como pontos fora do cone de luz, futuro causal ou passado causal.^[7]

Os pontos contidos em ${\displaystyle \,I^{+}(x)}$, por exemplo, podem ser alcançados a partir de ${\displaystyle x}$ por uma curva semelhante ao tempo direcionada ao futuro. O ponto ${\displaystyle x}$ pode ser alcançado, por exemplo, a partir de pontos contidos em ${\displaystyle \,J^{-}(x)}$ por uma curva que não é espacial direcionada ao futuro.

No espaço-tempo de Minkowski o conjunto ${\displaystyle \,I^{+}(x)}$ é o interior do cone de luz futuro em ${\displaystyle x}$. O conjunto ${\displaystyle \,J^{+}(x)}$ é o cone de luz futuro completo em ${\displaystyle x}$, incluindo o próprio cone.

Esses conjuntos ${\displaystyle \,I^{+}(x),I^{-}(x),J^{+}(x),J^{-}(x)}$ definidos para todo ${\displaystyle x}$ em ${\displaystyle M}$, são chamados coletivamente de estrutura causal de ${\displaystyle M}$.

Para ${\displaystyle S}$, um subconjunto de ${\displaystyle M}$, definimos^[5]

${\displaystyle I^{\pm }[S]=\bigcup _{x\in S}I^{\pm }(x)}$

${\displaystyle J^{\pm }[S]=\bigcup _{x\in S}J^{\pm }(x)}$

Para ${\displaystyle S,T}$ dois subconjuntos de ${\displaystyle M}$ definimos

• O futuro cronológico de ${\displaystyle S}$ relativo a ${\displaystyle T}$, ${\displaystyle I^{+}[S;T]}$, é o futuro cronológico de ${\displaystyle S}$ considerado como uma subvariedade de ${\displaystyle T}$. Observe que este é um conceito bem diferente de ${\displaystyle I^{+}[S]\cap T}$ que fornece o conjunto de pontos em ${\displaystyle T}$ que pode ser alcançado por curvas semelhantes ao tempo direcionadas ao futuro começando em ${\displaystyle S}$. No primeiro caso, as curvas devem estar em ${\displaystyle T}$, no segundo caso, não. Veja Hawking e Ellis.
• O futuro causal de ${\displaystyle S}$ relativo a ${\displaystyle T}$, ${\displaystyle J^{+}[S;T]}$, é o futuro causal de ${\displaystyle S}$ considerado como uma subvariedade de ${\displaystyle T}$. Observe que este é um conceito bem diferente de ${\displaystyle J^{+}[S]\cap T}$ que fornece o conjunto de pontos em ${\displaystyle T}$ que pode ser alcançado por curvas causais direcionadas ao futuro começando em ${\displaystyle S}$. No primeiro caso, as curvas devem estar em ${\displaystyle T}$, no segundo caso, não. Veja Hawking e Ellis.
• Um conjunto futuro é um conjunto fechado sob o futuro cronológico.
• Um conjunto passado é um conjunto fechado sob o passado cronológico.
• Um conjunto passado indecomponível (P.I.)^[a] é um conjunto passado que não é a união de dois subconjuntos próprios passados abertos diferentes.
• Um P.I. que não coincide com o passado de qualquer ponto em ${\displaystyle M}$ é chamado de conjunto passado indecomponível terminal (P.I.T.)^[b].
• Um conjunto passado indecomponível própeio (P.I.P.)^[c] é um P.I. que não é um P.I.T. ${\displaystyle I^{-}(x)}$ é um conjunto passado indecomponível adequado (P.I.P.).
• O desenvolvimento de Cauchy [en] futuro de ${\displaystyle S}$, ${\displaystyle D^{+}(S)}$ é o conjunto de todos os pontos ${\displaystyle x}$ para os quais toda curva causal inextensível direcionada ao passado através de ${\displaystyle x}$ intercepta ${\displaystyle S}$ pelo menos uma vez. Da mesma forma para o desenvolvimento passado de Cauchy. O desenvolvimento de Cauchy é a união dos desenvolvimentos de Cauchy do futuro e do passado. Os desenvolvimentos de Cauchy são importantes para o estudo do determinismo.
• Um subconjunto ${\displaystyle S\subset M}$ é acronal se não existir ${\displaystyle q,r\in S}$ tal que ${\displaystyle r\in I^{+}(q)}$, ou equivalentemente, se ${\displaystyle S}$ for disjunto de ${\displaystyle I^{+}[S]}$.

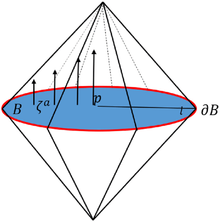
• Uma superfície de Cauchy [en] é um conjunto acronal fechado cujo desenvolvimento de Cauchy é ${\displaystyle M}$.
• Uma métrica é globalmente hiperbólica se puder ser folheada por superfícies de Cauchy.
• O conjunto de violação de cronologia é o conjunto de pontos através dos quais passam curvas fechadas semelhantes ao tempo.
• O conjunto de violação de causalidade é o conjunto de pontos pelos quais passam as curvas causais fechadas.
• O limite do conjunto de violação de causalidade é um horizonte de Cauchy. Se o horizonte de Cauchy for gerado por geodésicas nulas fechadas, haverá um fator de desvio para o vermelho associado a cada uma delas.
• Para uma curva causal ${\displaystyle \gamma }$, o diamante causal é ${\displaystyle J^{+}(\gamma (t_{1}))\cap J^{-}(\gamma (t_{2}))}$ (aqui estamos usando uma definição mais ampla de "curva" na qual é apenas um conjunto de pontos), sendo o ponto ${\displaystyle \gamma (t_{1})}$ no passado causal de ${\displaystyle \gamma (t_{2})}$. Em palavras: o diamante causal da linha de mundo de uma partícula ${\displaystyle \gamma }$ é o conjunto de todos os eventos que se encontram no passado de algum ponto em ${\displaystyle \gamma }$ e no futuro de algum ponto em ${\displaystyle \gamma }$. Na versão discreta, o diamante causal é o conjunto de todos os caminhos causais que conectam ${\displaystyle \gamma (t_{2})}$ a partir de ${\displaystyle \gamma (t_{1})}$.

Propriedades

• Um ponto ${\displaystyle x}$ está em ${\displaystyle \,I^{-}(y)}$ se e somente se ${\displaystyle y}$ está em ${\displaystyle \,I^{+}(x)}$.
• ${\displaystyle x\prec y\implies I^{-}(x)\subset I^{-}(y)}$
• ${\displaystyle x\prec y\implies I^{+}(y)\subset I^{+}(x)}$
• ${\displaystyle I^{+}[S]=I^{+}[I^{+}[S]]\subset J^{+}[S]=J^{+}[J^{+}[S]]}$
• ${\displaystyle I^{-}[S]=I^{-}[I^{-}[S]]\subset J^{-}[S]=J^{-}[J^{-}[S]]}$
• O horismos é gerado por congruências geodésicas nulas.

Propriedades topológicas:

• ${\displaystyle I^{\pm }(x)}$ é aberto para todos os pontos ${\displaystyle x}$ em ${\displaystyle M}$.
• ${\displaystyle I^{\pm }[S]}$ é aberto para todos os subconjuntos ${\displaystyle S\subset M}$.
• ${\displaystyle I^{\pm }[S]=I^{\pm }[{\overline {S}}]}$ para todos os subconjuntos ${\displaystyle S\subset M}$. Aqui ${\displaystyle {\overline {S}}}$ é o fechamento de um subconjunto ${\displaystyle S}$.
• ${\displaystyle I^{\pm }[S]\subset {\overline {J^{\pm }[S]}}}$

Geometria conforme

Duas métricas ${\displaystyle \,g}$ and ${\displaystyle {\hat {g}}}$ são conformemente relacionadas^[8] se ${\displaystyle {\hat {g}}=\Omega ^{2}g}$ para alguma função real ${\displaystyle \Omega }$ chamada de fator conforme.

Observando as definições de quais vetores tangentes são semelhantes ao tempo, nulos (semelhantes à luz) e semelhantes ao espaço, vemos que eles permanecem inalterados se usarmos ${\displaystyle \,g}$ ou ${\displaystyle {\hat {g}}}$. Como exemplo, suponha que ${\displaystyle X}$ seja um vetor tangente semelhante ao tempo em relação à métrica ${\displaystyle \,g}$. Isso significa que ${\displaystyle \,g(X,X)<0}$. Temos então que ${\displaystyle {\hat {g}}(X,X)=\Omega ^{2}g(X,X)<0}$ então ${\displaystyle X}$ é um vetor tangente semelhante ao tempo em relação ao ${\displaystyle {\hat {g}}}$ também.

Segue-se disso que a estrutura causal de uma variedade lorentziana não é afetada por uma transformação conforme.

Uma geodésica nula permanece uma geodésica nula sob um redimensionamento conforme.

Infinito conforme

Uma métrica infinita admite geodésicas de comprimento infinito/tempo próprio. No entanto, às vezes podemos fazer um redimensionamento conforme da métrica com um fator conforme que cai suficientemente rápido para 0 à medida que nos aproximamos do infinito para obter o limite conforme da variedade. A estrutura topológica do limite conforme depende da estrutura causal.

• As geodésicas semelhantes ao tempo direcionadas para o futuro terminam em i + ${\displaystyle i^{+}}$, o infinito futuro semelhante ao tempo.
• Geodésicas semelhantes ao tempo direcionadas ao passado terminam em ${\displaystyle i^{-}}$, o infinito passado semelhante ao tempo.
• Geodésicas nulas (semelhantes à luz) direcionadas para o futuro terminam em ℐ⁺, o infinito futuro nulo [en] (semelhante à luz).
• Geodésicas nulas (semelhantes à luz) direcionadas ao passado terminam em ℐ⁻, o passado infinito nulo (semelhante à luz).

Em vários espaços:

• Espaço de Minkowski: ${\displaystyle i^{\pm }}$ são pontos, ℐ^± são folhas nulas e infinito semelhante ao espaço tem codimensão 2.
• Antiespaço de de Sitter [en]: não há infinito semelhante ao tempo ou nulo (semelhante à luz), e o infinito semelhante ao espaço tem codimensão 1.
• Espaço de de Sitter: o infinito futuro e passado semelhantes ao tempo tem codimensão 1.

Singularidade gravitacional

Se uma geodésica termina após um parâmetro afim finito e não é possível estender a variedade para estender a geodésica, então temos uma singularidade.

Para buracos negros, o limite futuro semelhante ao tempo termina em uma singularidade em alguns lugares.

Para o Big Bang, o limite passado semelhante ao tempo também é uma singularidade.

O horizonte de eventos absoluto é o cone nulo passado do infinito futuro semelhante ao tempo. É gerado por geodésicas nulas que obedecem à equação óptica de Raychaudhuri.

Ver também

• Conjuntos causais
• Curva semelhante ao tempo fechada
• Diagrama de Penrose
• Espaço-tempo
• Hipótese da censura cósmica
• Teoremas de singularidade de Penrose – Hawking

Notas

Referências

Bibliografia

• Hawking, S.W.; Ellis, G. F. R. (1973), The large scale structure of space–time, ISBN 0-521-20016-4 (em inglês), Cambridge: Cambridge university press 
• Hawking, S.W.; Israel, W. (1979), General relativity, an Einstein centenary survey, ISBN 0-521-22285-0 (em inglês), Cambridge university press 
• Penrose, R. (1972), Techniques of differential topology in relativity, ISBN 0898710057 (em inglês), SIAM 
• Sard, R. D. (1970). Relativistic mechanics - Special relativity and classical particle dynamics (em inglês). Nova Iorque: W. A. Benjamin. ISBN 978-0805384918 

Leitura adicional

Ligações externas

• Turing machine causal networks (de Enrique Zeleny, o Projeto de demonstrações da Wolfram, em inglês)
• Weisstein, Eric W. «Causal network» (em inglês). MathWorld