RLC回路

RLC回路（アールエルシーかいろ、英: RLC circuit）は、抵抗器 (R) 、コイル (L) 、コンデンサ (C) を直列または並列に接続した電気回路である。LCR回路、共振回路、同調回路とも呼ぶ。この構成によって調和振動子を形成する。

RLC回路はラジオや通信工学や発振回路で様々な応用がある。周波数の全スペクトルから特定の信号の狭い帯域幅を選択するのに使うこともできる。例えば、アナログ式のAMやFMラジオではRLC回路を選局に使っている。典型的な構成では、可変コンデンサが選局用ダイヤルに繋がっていて、Cの値を変化させることで同調する周波数を変化させる。

RLC回路の任意の箇所の電圧や電流は2階微分方程式で表せる。

構成

RLC回路は電源と共振部に分けられる。電源には電圧源と電流源がある。同様に共振部にもLC回路が直列のものと並列のものがある。結果としてRLC回路にはこれらを組み合わせた4種類が存在する。

  • 直列LC部と電圧源
  • 直列LC部と電流源
  • 並列LC部と電圧源
  • 並列LC部と電流源

電圧源と電流源は容易に相互に変換可能であるため、これらは結局2種類に分類できる。すなわち、「直列LC部と電圧源」と「並列LC部と電流源」の回路は双対回路である。同様に「直列LC部と電流源」と「並列LC部と電圧源」の回路も双対回路である。

直列回路と並列回路の類似点と差異

直列構成と並列構成の帯域幅の式は互いの逆の関係にある。このことは、回路設計でどちらを使うべきかを判断するのに便利である。しかし、回路解析においては、共振周波数とQ値をシステムの特性として使うことが多い。

基本パラメータ

RLC回路の動作を記述する基本的な2つのパラメータが存在する。それは、共振周波数と減衰（または減衰係数）である。これら2つから導出できる派生パラメータについても後述する。本項目では複素数の虚数単位について、iではなくjを用いる。

共振周波数

RLC回路の非減衰共振周波数は以下のようになる（単位はラジアン毎秒）。

ω 0 = 1 L C {\displaystyle \omega _{0}={1 \over {\sqrt {LC}}}}

より一般的なヘルツ（秒あたりの周期数）で表すと、次のようになる。

f 0 = ω 0 2 π = 1 2 π L C {\displaystyle f_{0}={\omega _{0} \over 2\pi }={1 \over 2\pi {\sqrt {LC}}}}

LC共振部の複素インピーダンス ZLC がゼロになると、共振が起きる。

Z L C = Z L + Z C = 0 {\displaystyle Z_{LC}=Z_{L}+Z_{C}=0\quad }

これらインピーダンスは角周波数 ω {\displaystyle \omega } の関数である。

Z C = 1 j ω C {\displaystyle Z_{C}={1 \over {j\omega C}}}
Z L = j ω L {\displaystyle Z_{L}=j\omega L\quad }

ω = ω 0 {\displaystyle \omega =\omega _{0}} のときインピーダンスの大きさがゼロになると設定し、 j 2 = − 1 {\displaystyle j^{2}=-1} を使うと次のようになる。

| Z L C | = ω 0 L − 1 ω 0 C = 0 {\displaystyle |Z_{LC}|=\omega _{0}L-{1 \over {\omega _{0}C}}=0}
ω 0 2 = 1 L C ⇒ ω 0 = 1 L C {\displaystyle \omega _{0}{}^{2}={1 \over {LC}}\Rightarrow \omega _{0}={1 \over {\sqrt {LC}}}}

減衰

減衰 α は次のように定義される。まず、直列RLC回路では次のようになる。

α = R 2 L {\displaystyle \alpha ={R \over 2L}}

そして、並列RLC回路では次のようになる。

α = 1 2 R C {\displaystyle \alpha ={1 \over 2RC}}

減衰係数

直列RLC回路の減衰係数 ζ は、共振周波数 ω0 で減衰 α を割った比である。

ζ = α ω 0 = R 2 C L {\displaystyle \zeta ={\alpha \over \omega _{0}}={R \over 2}{\sqrt {C \over L}}}

そして、並列RLC回路でも同様である。

ζ = α ω 0 = 1 2 R L C {\displaystyle \zeta ={\alpha \over \omega _{0}}={1 \over 2R}{\sqrt {L \over C}}}

減衰係数は次元がないため、共振回路を解析する際に減衰よりも扱いやすい場合がある。減衰の次元はラジアン毎秒である。

発振回路での減衰の最小化

発振回路に応用する場合、減衰（あるいは減衰係数）が小さければ小さいほど好ましい。実際、直列RLC回路の発振回路ではなるべく R を小さくし、並列RLC回路では R をなるべく大きくする。どちらの場合もRLC回路は理想的なLC回路のよい近似となる。

一方バンドパスフィルタに応用する場合、減衰係数の値をうまく選択することでフィルタの通過帯域幅を設定できる。帯域幅を広くするには減衰係数を大きくすればよい（逆も同様）。これは実際の回路では R と L の値を調整することでなされる。

派生パラメータ

派生パラメータとしては、帯域幅、Q値、減衰共振周波数などがある。

帯域幅

RLC回路は、同じ入力抵抗の受信回路と R を置換することでバンドパスフィルタやバンドストップフィルタとして使える。直列回路の場合の帯域幅（ラジアン毎秒）は次のようになる。

Δ ω = 2 α = 2 ζ ω 0 = R L {\displaystyle \Delta \omega =2\alpha =2\zeta \omega _{0}={R \over L}}

同様に帯域幅をヘルツで表すと次のようになる。

Δ f = Δ ω 2 π = α π = ζ ω 0 π = R 2 π L {\displaystyle \Delta f={\Delta \omega \over 2\pi }={\alpha \over \pi }={\zeta \omega _{0} \over \pi }={R \over 2\pi L}}

帯域幅は周波数応答がピークの半分になる2つの周波数の幅（通過帯域の幅、または阻止帯域の幅）である。

減衰共振

減衰共振周波数 (damped resonance frequency) は、共振周波数と減衰係数から導出される。不足減衰 (underdamping) の場合、すなわち

α < ω 0 {\displaystyle \displaystyle \alpha <\omega _{0}}

または等価的に

ζ < 1 {\displaystyle \displaystyle \zeta <1}

である場合、減衰共振を次のように定義できる。

ω d = ω 0 2 − α 2 = ω 0 1 − ζ 2 {\displaystyle \omega _{d}={\sqrt {\omega _{0}^{2}-\alpha ^{2}}}=\omega _{0}{\sqrt {1-\zeta ^{2}}}}

発振回路では、

α ≪ ω 0 {\displaystyle \alpha \ll \omega _{0}}

または

ζ ≪ 1 {\displaystyle \zeta \ll 1}

が成り立つ。従って、次のように近似できる。

ω d ≈ ω 0 {\displaystyle \omega _{d}\approx \omega _{0}}

回路解析

直列RLC回路と電圧源

この場合、全電子部品が電圧源と直列に接続される。

RLC直列回路
RLC直列回路

直列RLC回路の記号:

v, R, L, C をパラメータとして、電荷 q を求める。まずキルヒホッフの電圧則から、次が成り立つ。

v R + v L + v C = v {\displaystyle {v_{R}+v_{L}+v_{C}=v}\,}

電圧を時間の関数 v(t) とすると、次のようになる。

R i ( t ) + L d i d t + 1 C ∫ − ∞ t i ( τ ) d τ = v ( t ) {\displaystyle Ri(t)+L{{di} \over {dt}}+{1 \over C}\int _{-\infty }^{t}i(\tau )\,d\tau =v(t)}

電荷と電流の関係は次のように表せる。

i ( t ) = d q d t {\displaystyle i(t)={{dq} \over {dt}}}

すると、上の式をコンデンサの電荷で表すと、次のようになる。

L d 2 q d t 2 + R d q d t + 1 C q ( t ) = v ( t ) {\displaystyle L{{d^{2}q} \over {dt^{2}}}+{R}{{dq} \over {dt}}+{1 \over {C}}q(t)=v(t)}

両辺を L で割ると、次の2階微分方程式になる。

d 2 q d t 2 + R L d q d t + 1 L C q ( t ) = 1 L v ( t ) {\displaystyle {{d^{2}q} \over {dt^{2}}}+{R \over L}{{dq} \over {dt}}+{1 \over {LC}}q(t)={1 \over L}v(t)}

ここで、2つの基本パラメータを定義する。

ζ N = R 2 C L {\displaystyle \zeta _{N}={R \over 2}{\sqrt {C \over L}}} および ω 0 = 1 L C {\displaystyle \omega _{0}={1 \over {\sqrt {LC}}}}

これらを使って上の微分方程式の係数を置換すると、次のようになる。

d 2 q d t 2 + 2 ζ N . ω 0 d q d t + ω 0 2 q ( t ) = 1 L v ( t ) {\displaystyle {{d^{2}q} \over {dt^{2}}}+2\zeta _{N}.\omega _{0}{{dq} \over {dt}}+\omega _{0}^{2}q(t)={1 \over L}v(t)}

あるいは

q ″ + 2 ζ N . ω 0 q ′ + ω 0 2 q = 1 L v ( t ) {\displaystyle q''+2\zeta _{N}.\omega _{0}q'+\omega _{0}^{2}q={1 \over L}v(t)}

周波数領域

直列RLC回路を周波数領域で解析するには、複素インピーダンスを使う。電圧源が複素振幅 V(s) で角周波数 s = σ + i ω {\displaystyle s=\sigma +i\omega } の複素指数波形を生成するとき、キルヒホッフの電圧則を適用でき、次の式が得られる。

V ( s ) = I ( s ) ( R + L s + 1 C s ) {\displaystyle V(s)=I(s)\left(R+Ls+{\frac {1}{Cs}}\right)}

ここで、I(s) は全部品を流れる複素電流である。これを I(s) について解くと

I ( s ) = 1 R + L s + 1 C s V ( s ) {\displaystyle I(s)={\frac {1}{R+Ls+{\frac {1}{Cs}}}}V(s)}

となり、これを変形すると次のようになる。

I ( s ) = s L ( s 2 + R L s + 1 L C ) V ( s ) {\displaystyle I(s)={\frac {s}{L\left(s^{2}+{R \over L}s+{\frac {1}{LC}}\right)}}V(s)}

複素アドミッタンス

次に、複素アドミッタンス Y(s) を求める。

Y ( s ) = I ( s ) V ( s ) = s L ( s 2 + R L s + 1 L C ) {\displaystyle Y(s)={I(s) \over V(s)}={\frac {s}{L\left(s^{2}+{R \over L}s+{\frac {1}{LC}}\right)}}}

これに基本パラメータ α と ωo を使うと、次が得られる。

Y ( s ) = I ( s ) V ( s ) = s L ( s 2 + 2 α s + ω 0 2 ) {\displaystyle Y(s)={I(s) \over V(s)}={\frac {s}{L\left(s^{2}+2\alpha s+\omega _{0}^{2}\right)}}}

なお、この Y(s) の式は、零状態応答 (Zero State Response) の式と同じである。

極と零点

Y(s) の零点は、 Y ( s ) = 0 {\displaystyle Y(s)=0} となるような s の値である。

s = 0 {\displaystyle s=0\,}     かつ     | s | → ∞ {\displaystyle |s|\rightarrow \infty }

Y(s) の極は、 Y ( s ) → ∞ {\displaystyle Y(s)\rightarrow \infty } となるような s の値である。分母の二次方程式を解くと

s = − α ± α 2 − ω 0 2 {\displaystyle s=-\alpha \pm {\sqrt {\alpha ^{2}-\omega _{0}^{2}}}}

となる。なお、Y(s) の極は、特性多項式の根 λ 1 {\displaystyle \lambda _{1}} と λ 2 {\displaystyle \lambda _{2}} と同じである。

正弦波定常状態

ここで、 s = j ω {\displaystyle s=j\omega } とする。

上の式の絶対値（振幅成分）をとると、次のようになる。

| Y ( s = j ω ) | = 1 R 2 + ( ω L − 1 ω C ) 2 {\displaystyle |Y(s=j\omega )|={\frac {1}{\sqrt {R^{2}+\left(\omega L-{\frac {1}{\omega C}}\right)^{2}}}}}

次に電流の絶対値（振幅）を ω の関数として次のように表せる。

| I ( j ω ) | = | Y ( j ω ) | | V ( j ω ) | . {\displaystyle |I(j\omega )|=|Y(j\omega )||V(j\omega )|.\,}

R = 1 オーム、C = 1 ファラド、L = 1 ヘンリー、V = 1.0 ボルトとすると、電流 i （アンペア）の振幅を ω {\displaystyle \omega } (rad/s)の関数としてグラフに表すと、次のようになる。

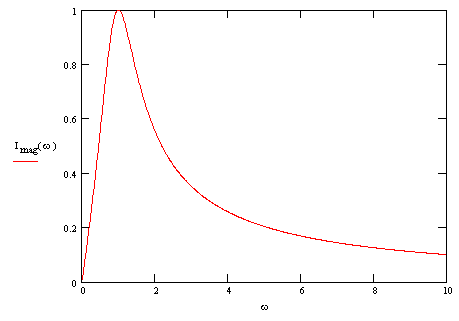正弦波定常状態解析
正弦波定常状態解析

見ての通り、 i m a g ( ω ) = 1 {\displaystyle i_{mag}(\omega )=1} となるピークがある。この点の周波数が共振周波数である。この値を求めると次のようになる。

ω 0 = 1 L C {\displaystyle \omega _{0}={\frac {1}{\sqrt {LC}}}}

並列RLC回路

RLC並列回路
RLC並列回路

並列RLC回路の記号:

この回路の複素アドミッタンスは各部品のアドミッタンスの総和で求められる。

1 Z = 1 Z L + 1 Z C + 1 Z R = 1 j ω L + j ω C + 1 R {\displaystyle {1 \over Z}={1 \over Z_{L}}+{1 \over Z_{C}}+{1 \over Z_{R}}={1 \over {j\omega L}}+{j\omega C}+{1 \over R}}

また、この回路の複素インピーダンスは、各部品の複素インピーダンス全体の並列（英語版）で求められる。

Z = Z L ∥ Z C ∥ Z R = j ω L ∥ 1 j ω C ∥ R {\displaystyle Z={Z_{L}}\parallel {Z_{C}}\parallel {Z_{R}}={j\omega L}\parallel {\frac {1}{j\omega C}}\parallel {R}}

直列配置と並列配置の違いは、その動作にも直接関係する。電流 I = V Z {\displaystyle I={V \over Z}} をグラフで描画してみるとそれが一目でわかる。比較のため、上のグラフと同じように R = 1 オーム、C = 1 ファラド、L = 1 ヘンリー、V = 1.0 ボルトとし、ω をラジアン毎秒としたグラフが下図である。

電流が最小になる周波数が共振周波数であり ω 0 = 1 L C {\displaystyle \omega _{0}={1 \over {\sqrt {LC}}}} である。

並列RLC回路はバンドストップ回路応答を示し、共振周波数付近の帯域をブロックするフィルタの役目を果たす。

関連項目

外部リンク

  • a treatment that starts with the mechanical analogy
  • An interactive simulation on series RCL circuit
  • Interactive Visual Representation of the LRC Circuit
  • Pulse Response Examiner freeware (Windows)
  • RLC直列回路
典拠管理データベース: 国立図書館 ウィキデータを編集
  • ドイツ