レンズの公式(レンズのこうしき)は幾何光学における公式であり、
- 物面から主点までの距離 A
- 主点から像面までの距離 B
- 焦点距離 F (主点と焦点の距離)
の関係が理想的には と表されるというものである。ただし、焦点距離 F は凹レンズなどの発散系では負とし、像面までの距離 B は虚像では負とする。物が無限遠にある場合は左辺第1項を0、像が無限遠方の虚像である場合は左辺第2項を0として成立する。
と表されるというものである。ただし、焦点距離 F は凹レンズなどの発散系では負とし、像面までの距離 B は虚像では負とする。物が無限遠にある場合は左辺第1項を0、像が無限遠方の虚像である場合は左辺第2項を0として成立する。
この公式は単レンズだけでなく凹面鏡・凸面鏡や、複数のレンズ・鏡を組み合わせた光学系にも(主点・焦点が定義できるならば)適用できる。
レンズメーカーの公式
空気中にある単レンズの焦点距離は以下の式から計算できる[要出典]。
![{\displaystyle {\frac {1}{F}}=(n-1)\left[{\frac {1}{R_{1}}}-{\frac {1}{R_{2}}}+{\frac {(n-1)d}{nR_{1}R_{2}}}\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f2a764fbb1a4605be0fddc8e2a4003715b93b3a)
 はレンズの屈折率。
はレンズの屈折率。 はレンズ第1面の曲率半径。
はレンズ第1面の曲率半径。 はレンズ第2面の曲率半径。
はレンズ第2面の曲率半径。 はレンズの厚さ。
はレンズの厚さ。
この式はレンズメーカーの公式と呼ばれる。曲率半径は、曲率中心が光源から遠い方にある場合を正とする。
証明
以下の説明図ではレンズの中で光が曲がっているが、実際にはレンズに光が入るときと出るときの2回、屈折する。 また、式中の記号はすべて図中の点または長さをさす。
凸レンズに関する証明
焦点の外側に物体がある場合
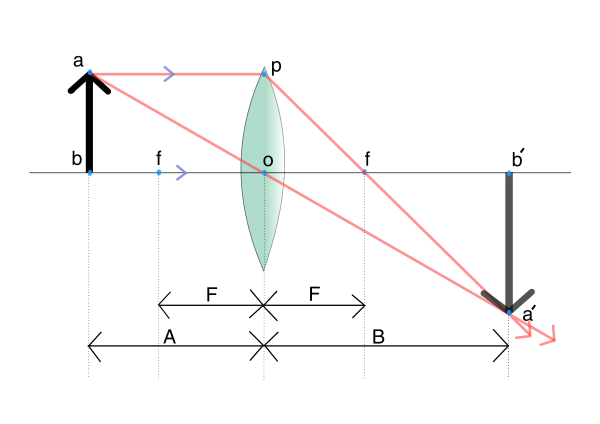 凸レンズの焦点より外側に物体を置くと、物体に対して反対側に倒立の実像ができる。
凸レンズの焦点より外側に物体を置くと、物体に対して反対側に倒立の実像ができる。 (証明)
 と
と  が相似であることより
が相似であることより

と言え、また  と
と  が相似であることより
が相似であることより

と言える。  であるから
であるから

となり、これを  で割ると
で割ると

(証明終わり)
焦点の内側に物体がある場合
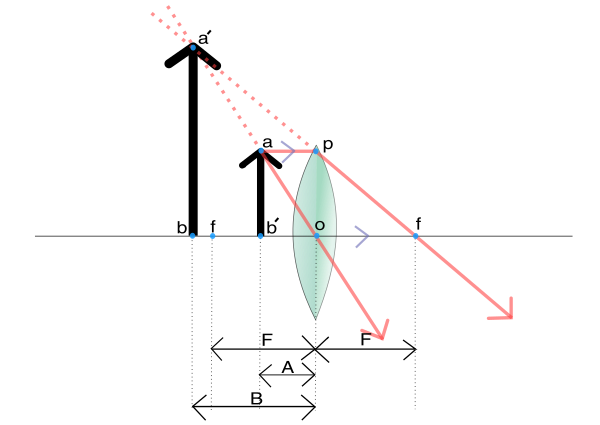 凸レンズの焦点より内側に物体を置くと、物体と同じ側に正立の虚像ができる。
凸レンズの焦点より内側に物体を置くと、物体と同じ側に正立の虚像ができる。 (証明)
 と
と  が相似であることより、
が相似であることより、

と言え、また  と
と (注を参照のこと) が相似であることより、
(注を参照のこと) が相似であることより、

と言える。  であるから、
であるから、

となり、これを  で割ると、
で割ると、

像が虚像であるため B を負の数で表し B' = -B とおくと、上式は

となる。
(証明終わり) (注)図中には、fが2点あるが、右側のfをさす。
凹レンズに関する証明
 凹レンズでは物体と同じ側に正立の虚像ができる。
凹レンズでは物体と同じ側に正立の虚像ができる。 (証明)
 と
と  が相似であることより、
が相似であることより、

と言え、また  と
と  が相似であることより、
が相似であることより、

と言える。ところで、  であるから、
であるから、

となり、これを  で割ると、
で割ると、

凹レンズによる虚像であるため B, F を負の数で表し F' = -F; B' = -B とおくと、上式は

となる。
(証明終わり)
レンズフレアの公式
レンズに入射した光の一部はレンズ内面で一回もしくは複数回反射する。これがレンズフレアの原因のひとつである。凸レンズ内を  回反射したときの焦点距離は
回反射したときの焦点距離は

 はレンズの(零回反射の)焦点距離
はレンズの(零回反射の)焦点距離 はレンズの屈折率
はレンズの屈折率
で与えられる[1]。 ここで負の焦点距離は焦点がレンズ前方にあることを意味する。
典型的な  と
と  の場合を計算すれば、一回反射の焦点距離公式
の場合を計算すれば、一回反射の焦点距離公式

及び二回反射の焦点距離公式

が得られる。
熊本県立宇土高等学校科学部は、このレンズ内反射による結像の現象を再発見し、前述の両凸レンズ、平凸レンズ、凸平レンズに対する一回反射と二回反射による結像距離の公式を与えた[2]。例えば、両凸レンズの場合には、上記の焦点距離公式から

及び

が得られる。同研究ではレンズ内反射による実像は「副実像」と呼ばれている。同研究は国内メディアで報道され[3]、高校物理の教科書にも採用された[4]。
脚注
[脚注の使い方]
- ^ Jacobson, Ralph; Ray, Sidney; Attridge, Geoffrey G.; Axford, Norman (2000). Manual of Photography (9th ed.). Routledge. doi:10.4324/9780080510965 p. 68
- ^ “"副実像"の写像公式化の研究”. 熊本県立宇土高等学校. 2022年3月5日閲覧。
- ^ “常識を覆す大発見! 実像・虚像に続く「新たな像」見つけた 熊本県立宇土高校科学部物理班”. 高校生新聞 (2014年). 2022年7月5日閲覧。
- ^ “宇土高研究 教科書に”. 熊本日日新聞 (2017年). 2022年7月5日閲覧。
関連項目




![{\displaystyle {\frac {1}{F}}=(n-1)\left[{\frac {1}{R_{1}}}-{\frac {1}{R_{2}}}+{\frac {(n-1)d}{nR_{1}R_{2}}}\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f2a764fbb1a4605be0fddc8e2a4003715b93b3a)













































