Densità di un grafo

La densità di un grafo, indicata con Δ , {\displaystyle \Delta ,} è il rapporto tra il numero di archi del grafo rispetto al numero di coppie di nodi. Quindi misura quanti archi ha il grafo rispetto a quanti ne potrebbe avere dati i nodi del grafo.

Definizione

Sia definito il grafo G = ( N , A ) {\displaystyle G=(N,A)} come coppia dei due insiemi N := { 1 , 2 , 3 , … , n } {\displaystyle N:=\{1,2,3,\ldots ,n\}} ed A {\displaystyle A} sottinsieme del prodotto cartesiano N × N . {\displaystyle N\times N.} L'insieme N {\displaystyle N} è l'insieme dei nodi che compongono il suddetto grafo e A {\displaystyle A} è l'insieme degli archi. Sia n {\displaystyle n} la cardinalità di N {\displaystyle N} (ossia il numero dei nodi di un dato) e sia L {\displaystyle L} la cardinalità di A {\displaystyle A} (ossia il numero degli archi dello stesso grafo). Se le coppie di nodi si considerano ordinate il grafo è detto orientato o digrafo, altrimenti non orientato o semplice. Il grafo è detto pesato se ad ogni arco è associato un peso o costo.

La densità di un grafo semplice o non orientato è definita come:

Δ = 2 L n ( n − 1 ) . {\displaystyle \Delta ={\frac {2L}{n(n-1)}}.}

La densità di un grafo orientato è definita come:

Δ = L n ( n − 1 ) . {\displaystyle \Delta ={\frac {L}{n(n-1)}}.}

Nel caso di grafi pesati, ad L {\displaystyle L} occorre sostituire la sommatoria dei pesi di ciascun arco.

La densità di un grafo assume valori compresi tra 0 ed 1 e pertanto si può ricollegare facilmente al concetto di probabilità. La densità di un grafo misura la probabilità che una qualsiasi coppia di nodi sia adiacente, mentre la connessione di un grafo dipende dalla distribuzione degli archi tra i nodi.

Esempi

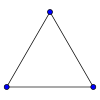
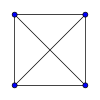
Grafi completi non orientati

Si abbia un grafo completo non orientato K n {\displaystyle K_{n}} con n = 1 , 2 , 3 , … , 8. {\displaystyle n=1,2,3,\ldots ,8.}


K 1 {\displaystyle K_{1}}
K 2 {\displaystyle K_{2}}
K 3 {\displaystyle K_{3}}
K 4 {\displaystyle K_{4}}

K 5 {\displaystyle K_{5}}
K 6 {\displaystyle K_{6}}
K 7 {\displaystyle K_{7}}
K 8 {\displaystyle K_{8}}

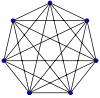La densità del grafo completo monopartito K n {\displaystyle K_{n}} è sempre 1.

Grafi bipartiti

Supponiamo di considerare il seguente grafo non orientato ciclico (detto grafo bipartito):

È possibile facilmente verificare che la sua densità è circa uguale a 0,28.

Applicazione alle reti sociali

Un gruppo di individui tra cui esistano o meno delle relazioni è rappresentabile matematicamente attraverso un grafo. Anche più gruppi di individui sono schematizzabili in egual maniera.

In generale:

  1. Diversi attori (entità sociali) instaurano o meno tra loro delle relazioni.
  2. Gli attori non coincidono necessariamente con le singole persone, ma possono essere enti, città, nazioni, ecc.
  3. Le relazioni possono essere di tipo emozionale (amicizia, amore, autorità, discendenza, rapporti di lavoro) oppure possono esprimere connessioni fisiche (ponti, strade) o ancora trasferimenti di risorse.

La densità nel grafo che rappresenta una rete sociale può essere un parametro che rappresenta l'efficienza nello scambio di informazioni e l'utilità per i singoli individui. Nelle opere di Mark Granovetter inoltre è evidenziato come reti piccole e dense possono essere meno utili di reti costituite da legami deboli, perché queste ultime sono più flessibili prestandosi quindi a un miglior scambio di idee e opportunità.

Bibliografia

  • Paul E. Black, Sparse graph, from Dictionary of Algorithms and Data Structures, Paul E. Black (ed.), NIST. Retrieved on 29 September 2005.
  • Thomas F. Coleman e Jorge J. Moré, Estimation of sparse Jacobian matrices and graph coloring Problems, in SIAM Journal on Numerical Analysis, vol. 20, n. 1, 1983, pp. 187–209, DOI:10.1137/0720013.
  • Reinhard Diestel, Graph Theory, Graduate Texts in Mathematics, Springer-Verlag, 2005, ISBN 3-540-26183-4, OCLC 181535575.
  • Bruno Preiss, Data Structures and Algorithms with Object-Oriented Design Patterns in C++, John Wiley & Sons, 1998, ISBN 0-471-24134-2.
  • I. Streinu e L. Theran, Sparse hypergraphs and pebble game algorithms, in European Journal of Combinatorics (special issue for Oriented Matroids '05), 2008, arΧiv:math/0703921.

Voci correlate

  • Rete sociale
  • Teoria dei grafi
  Portale Matematica
  Portale Sociologia