Gompertz-függvény

A Gompertz-függvény, vagy Gompertz-görbe egy szigmoid függvény. A függvényt Benjamin Gompertz (1779–1865), brit matematikusról nevezték el. A Gompertz-függvény egy matematikai modell, olyan időben zajló folyamatokra, ahol a folyamat kezdete és a vége lassú lecsengésű. A görbe jobb oldali, jövőbeli alakulása jóval fokozatosabb, mint a bal oldali, kezdeti szakaszé, szemben a logisztikai-függvénnyel, mely szintén egy szigmoid függvény, és ahol a görbe aszimptotái szimmetrikusak.

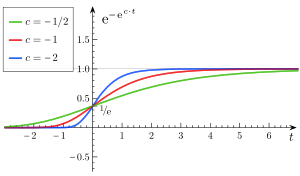
Az ábrákon három Gompertz-görbe látható, ahol az egyik változót megváltoztatják, míg a többi konstans változatlan.

Képlet

${\displaystyle y(t)=ae^{be^{ct}}}$

ahol

• a a felső aszimptota, mivel ${\displaystyle ae^{be^{-\infty }}=ae^{0}=a}$
• b, c negatív számok
• b beállítja az x eltolást
• c beállítja a növekedési rátát (x skálázása)
• e Euler-féle szám (e = 2,71828...)

A Gompertz-függvény a Gompertz-féle mortalitási törvényből eredeztethető, mely azt állítja, hogy a mortalitás (elmúlás, hanyatlás) exponenciálisan viselkedik. Matematikai függvénnyel kifejezve:

${\displaystyle k^{r}\propto {\frac {1}{y(t)}}}$

ahol

• ${\displaystyle r={\frac {y'(t)}{y(t)}}}$ a növekedési ráta.
• k egy tetszőleges konstans

Példák

Néhány példa a Gompertz-függvény alkalmazására:

• Behatárolt populáció esetén, ahol a születési arányok a kezdetben nőnek, majd lelassulnak, ahogy a források elérnek egy korlátot
• Tumorok növekedésének modellezése
• Mobil telefonok használatánál, ahol a költségek a kezdetben magasak (a használatba vétel lassú), és ezt követi egy gyors növekedés, majd lassul a használat, és eléri a telítődést.

Tumorok növekedése és a Gompertz-függvény

A 60-as években A.K. Laird^[1] használta először a Gompertz-függvényt tumorok növekedésének vizsgálatánál. A tumorok behatárolt területeken növekvő sejtpopulációk, ahol a tápanyag korlátozott. Legyen X(t) a tumor mérete, fel lehet írni a következő Gompertz-függvényt:

${\displaystyle X(t)=K\exp \left(\log \left({\frac {X(0)}{K}}\right)\exp \left(-\alpha t\right)\right)}$

ahol

• X(0) a tumor mérete a megfigyelés kezdetén;
• K a szállító kapacitás, azaz az elérhető maximális méret a rendelkezésre álló tápanyag mellett.

Ekkor:

${\displaystyle \lim _{t\rightarrow +\infty }X(t)=K}$

függetlenül ettől: X(0)>0. Megjegyezzük, hogy terápia hiányában az X(0)<K, miközben terápia mellett, X(0)>K lehet;

• α egy konstans, mely a sejtek burjánzási képességével kapcsolatos
• log( ) a természetes logaritmust jelenti

A Gompertz-függvény differenciálásakor, könnyű látni az X(t) dinamikáját:

${\displaystyle X^{\prime }(t)=\alpha \log \left({\frac {K}{X(t)}}\right)X(t)}$

azaz:

${\displaystyle X^{\prime }(t)=F\left(X(t)\right)X(t),F^{\prime }(X)\leq 0}$

ahol F(X) a pillanatnyi sejt burjánzási arány, melynek csökkenő természete a tápanyagért folyó versennyel kapcsolatos, ahogy a populáció nő, hasonlóan a logisztikai növekedési arányhoz. Azonban van egy alapvető különbség: logisztikai esetben, kis sejt populációkra a burjánzási sebesség véges:

${\displaystyle F(X)=\alpha \left(1-\left({\frac {X}{K}}\right)^{\nu }\right)\Rightarrow F(0)=\alpha <+\infty }$

míg, a Gompertz esetben a burjánzás korlátok nélküli:

${\displaystyle \lim _{X\rightarrow 0^{+}}F(X)=\lim _{X\rightarrow 0^{+}}\alpha \log \left({\frac {K}{X}}\right)=+\infty }$

Steel^[2] és Wheldon^[3] megállapítja, hogy a sejtburjánzási sebesség egy populációban korlátozva van a sejtosztódási idő által. Ily módon ez egy bizonyíték lehet arra, hogy a Gompertz-függvény nem jó modell kis tumorok esetében. Mindezen túl megállapították,^[4] hogy az immunrendszert is figyelembe véve, Gompertz- és más törvények, melyekre a korlátlanság F(0) jellemző, kizárhatják az immunrendszer működésének a lehetőségét.

Gompertz-, és a logisztikai növekedés

A Gompertz differenciális egyenlet:

${\displaystyle X^{\prime }(t)=\alpha \log \left({\frac {K}{X(t)}}\right)X(t)}$

ez az általános logisztikai függvény korlátozott esete

${\displaystyle X^{\prime }(t)=\alpha \nu \left(1-\left({\frac {X(t)}{K}}\right)^{\frac {1}{\nu }}\right)X(t)}$

ahol ${\displaystyle \nu >0}$ egy pozitív valós szám ezért:

${\displaystyle \lim _{\nu \rightarrow +\infty }\nu \left(1-x^{1/\nu }\right)=-\log \left(x\right)}$.

Ráadásul, az általános logisztikai függvény görbéjén van egy inflekciós pont, amikor

${\displaystyle X(t)=\left({\frac {\nu }{\nu +1}}\right)^{\nu }K}$

és egy a Gompertz-függvényen, amikor

${\displaystyle X(t)={\frac {K}{e}}=K\cdot \lim _{\nu \rightarrow +\infty }\left({\frac {\nu }{\nu +1}}\right)^{\nu }}$.

A növekedés Gomp-ex törvénye

A fenti megállapításokra alapozva Wheldon^[3] javasolt egy matematikai modellt a tumorok növekedésére, melyet Gomp-Ex modellnek nevezett el, kissé különbözik a Gormpertz-törvénytől. A Gomp-Ex modell feltételezi, hogy a kezdetben nincs verseny a forrásokért, így a sejt populációk az exponenciális törvény szerint viselkednek. Azonban van egy kritikus határérték ${\displaystyle X_{C}}$, ${\displaystyle X>X_{C}}$-re, ahol a növekedés a Gompertz-törvény szerint zajlik:

${\displaystyle F(X)=\max \left(a,\alpha \log \left({\frac {K}{X}}\right)\right)}$

így:

${\displaystyle X_{C}=K\exp \left(-{\frac {a}{\alpha }}\right).}$

Néhány numerikus becslés az ${\displaystyle X_{C}}$-re^[3]

• ${\displaystyle X_{C}\approx 10^{9}}$ emberi tumorokra
• ${\displaystyle X_{C}\approx 10^{6}}$ egér tumorokra

Irodalom

• Wheldon, T.E: Mathematical Models in Cancer Research. (hely nélkül): Bristol: Adam Hilger. 1988.  
• d'Onofrio A: A general framework for modeling tumor-immune system competition and immunotherapy: Mathematical analysis and biomedical inferences. (hely nélkül): Physica D. 2005. 220–235. o.  

Kapcsolódó szócikkek

• Statisztika
• Demográfia
• Derivált
• Logisztikai-függvény
• Gompertz-eloszlás

További információk

• A Gompertz-függvényről a MathWorld-ön

Jegyzetek