Relations d'Euler dans le triangle

Les relations d'Euler dans le triangle sont des relations entre les rayons des cercles inscrit/exinscrits et circonscrit. Leonhard Euler les a publiées en 1767 ^[1],[2],[3], mais elles l'avaient déjà été par William Chappie en 1746^[4].

Notons qu'on désigne aussi par relation d'Euler la relation vectorielle ${\displaystyle {\overrightarrow {OH}}=3{\overrightarrow {OG}}}$ reliant le centre de gravité, l'orthocentre et le centre du cercle circonscrit.

Énoncé des relations

Pour un triangle quelconque, on note O, I, I_A les centres respectifs des cercles circonscrit, inscrit, et exinscrit dans l'angle ${\displaystyle {\widehat {A}}}$ (par exemple), et R, r, r_A leurs rayons respectifs.

Les relations d'Euler s'énoncent

ce qui peut aussi s'écrire :

ou encore :

On en déduit l'inégalité d'Euler ^[5]:

${\displaystyle R\geqslant 2r}$

laquelle est une égalité ssi le triangle est équilatéral ^[6].

Démonstrations

Première démonstration géométrique

Cette démonstration utilise la propriété suivante des puissances d'un point par rapport à deux cercles^[7],[8],[9]. Étant donnés deux cercles de centres O et O', et un point M se projetant en H sur l'axe radical, la différence des puissances de M par rapport aux deux cercles vérifie : ${\displaystyle P_{O}(M)-P_{O'}(M)=2{\overrightarrow {OO'}}\cdot {\overrightarrow {HM}}}$.

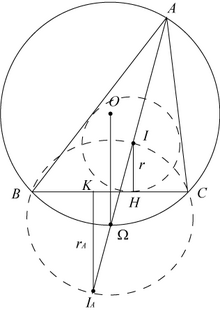
Dans le triangle ABC, les bissectrices (BI) et (BI_A) étant perpendiculaires ainsi que (CI) et (CI_A), le quadrilatère BICI_A est inscriptible dans un cercle de centre Ω, milieu du diamètre [II_A].

Désignons par Ω' le point d'intersection de la bissectrice issue de A avec le cercle circonscrit ; par le théorème de l'angle inscrit Ω' est le milieu de l'arc ${\displaystyle {\overset {\frown }{BC}}}$ donc ${\displaystyle \Omega 'B=\Omega 'C}$. Mais ${\displaystyle \Omega B=\Omega C}$ également, donc Ω = Ω', et Ω appartient au cercle circonscrit.

D'après la propriété ci-dessus, ${\displaystyle P_{O}(I)-P_{\Omega }(I)=2{\overrightarrow {O\Omega }}\cdot {\overrightarrow {HI}}=-2Rr}$.

Or ${\displaystyle P_{O}(I)=IO^{2}-R^{2}}$ et ${\displaystyle P_{\Omega }(I)=0}$, donc ${\displaystyle IO^{2}=R^{2}-2Rr}$.

De même, ${\displaystyle P_{O}(I_{A})-P_{\Omega }(I_{A})=2{\overrightarrow {O\Omega }}\cdot {\overrightarrow {KI}}=-2Rr_{A}}$.

D'après la propriété ci-dessus, ${\displaystyle P_{O}(I_{A})-P_{\Omega }(I_{A})=2{\overrightarrow {O\Omega }}\cdot {\overrightarrow {KI_{A}}}=2Rr_{A}}$.

Or ${\displaystyle P_{O}(I_{A})=I_{A}O^{2}-R^{2}}$ et ${\displaystyle P_{\Omega }(I_{A})=0}$, donc ${\displaystyle I_{A}O^{2}=R^{2}+2Rr_{A}}$.

Deuxième démonstration géométrique

Cette démonstration utilise les propriétés de l'angle inscrit et de la puissance d'un point par rapport à un cercle ^[10].

La droite (AI) coupe le cercle circonscrit en L. Soit M le point diamétralement opposé à L sur ce cercle.

Soit D le pied de la perpendiculaire menée de I sur (AB). C'est un point de tangence du cercle inscrit, en sorte qu'on a ID = r.

Les angles ${\displaystyle {\widehat {LAB}}}$ et ${\displaystyle {\widehat {LMB}}}$ sont égaux, puisqu'ils soutiennent le même arc capable. Les triangles rectangles IAD et LMB sont donc semblables puisqu'ils ont un angle non droit identique.

On en déduit : ID/LB = AI/LM, d'où ML × ID = AI × LB, et par conséquent : 2 R r = AI × LB.

D'autre part l'angle ${\displaystyle {\widehat {LIB}}}$ est le supplémentaire de l'angle ${\displaystyle {\widehat {AIB}}}$, c'est donc la somme des angles ${\displaystyle {\widehat {IAB}}}$ et ${\displaystyle {\widehat {IBA}}}$, soit la demi-somme des angles ${\displaystyle {\widehat {CAB}}}$ et ${\displaystyle {\widehat {CBA}}}$ et l'angle ${\displaystyle {\widehat {IBL}}}$ est la somme des angles ${\displaystyle {\widehat {IBC}}}$ et ${\displaystyle {\widehat {CBL}}}$, soit la somme des angles ${\displaystyle {\widehat {IBC}}}$ et ${\displaystyle {\widehat {CAL}}}$ (par propriété de l'angle inscrit), soit aussi la demi-somme des angles ${\displaystyle {\widehat {CAB}}}$ et ${\displaystyle {\widehat {CBA}}}$.

Le triangle BIL est donc isocèle, et par conséquent BL = LI, et : 2 R r = AI × LI.

Or, selon la propriété de la puissance d'un point par rapport à un cercle, puisque que I est intérieur au cercle, ${\displaystyle IA\times IL=R^{2}-OI^{2}}$.

Par conséquent : ${\displaystyle R^{2}-OI^{2}=2Rr}$, soit ${\displaystyle OI^{2}=R^{2}-2rR=R(R-2r)\,}$, ce qu'il fallait démontrer.

Note : une démonstration similaire mais plus générale puisqu'elle permet d'obtenir à la fois OI et OI_A, se trouve dans^[11].

Démonstration calculatoire

Le point I ayant pour coordonnées barycentriques ${\displaystyle (a,b,c)}$, on a

${\displaystyle (a+b+c){\overrightarrow {OI}}=a{\overrightarrow {OA}}+b{\overrightarrow {OB}}+c{\overrightarrow {OC}}}$.

D'où, en utilisant le théorème de l'angle au centre :

${\displaystyle (a+b+c)^{2}OI^{2}=(a^{2}+b^{2}+c^{2})R^{2}+2abR^{2}\cos 2{\widehat {C}}+2bcR^{2}\cos 2{\widehat {A}}+2acR^{2}\cos 2{\widehat {B}}}$.

Or

${\displaystyle \cos 2{\widehat {C}}=1-2\sin ^{2}{\widehat {C}}}$, etc.,

donc

${\displaystyle (a+b+c)^{2}OI^{2}=R^{2}[(a+b+c)^{2}-4ab\sin ^{2}{\widehat {C}}-4bc\sin ^{2}{\widehat {A}}-4ca\sin ^{2}{\widehat {B}}]}$.

Comme ${\displaystyle 2S=ab\sin {\widehat {C}}}$ et ${\displaystyle 4RS=abc}$, on a ${\displaystyle 4ab\sin ^{2}{\widehat {C}}=4c{\frac {S}{R}}}$, etc.

Donc

${\displaystyle (a+b+c)^{2}OI^{2}=R^{2}\left[(a+b+c)^{2}-4{\frac {S}{R}}(a+b+c)\right]}$.

Comme ${\displaystyle 2S=r(a+b+c)}$, on obtient ${\displaystyle OI^{2}=R^{2}\left(1-2{\frac {r}{R}}\right)=R(R-2r)}$.

La relation pour le cercle exinscrit s'obtient similairement en utilisant ${\displaystyle (-a+b+c){\overrightarrow {OI_{A}}}=-a\,{\overrightarrow {OA}}+b\,{\overrightarrow {OB}}+c\,{\overrightarrow {OC}}}$.

Problème réciproque

Étant donné un cercle ${\displaystyle C_{O}}$ de centre ${\displaystyle O}$ et de rayon ${\displaystyle R}$, et un cercle ${\displaystyle C_{I}}$ de centre ${\displaystyle I}$ et de rayon ${\displaystyle r}$ vérifiant ${\displaystyle OI^{2}=R(R-2r)}$, existe-t-il un triangle dont les cercles circonscrit et inscrit soient ${\displaystyle C_{O}}$ et ${\displaystyle C_{I}}$ ?

Non seulement la réponse est positive, mais d'après le porisme de Poncelet, le premier sommet du triangle peut être choisi quelconque sur ${\displaystyle C_{O}}$ ^[12],[9].

Notons que le cercle ${\displaystyle C_{I}}$ est intérieur au cercle ${\displaystyle C_{O}}$ car ${\displaystyle OI={\sqrt {R^{2}-2r}}\leqslant {\sqrt {(R-r)^{2}}}=R-r}$.

Voir aussi

• Théorème de Fuss (analogue pour le quadrilatère)
• Polygone bicentrique, où se trouvent des formules pour les polygones d'ordre 5, 6, 8.
• Porisme de Poncelet
• Liste de sujets portant le nom d'Euler

Références

• Portail de la géométrie