Processus ponctuel

En probabilité et statistique, un processus ponctuel est un type particulier de processus stochastique pour lequel une réalisation est un ensemble de points isolés du temps et/ou de l'espace. Par exemple, la position des arbres dans une forêt peut être modélisée comme la réalisation d'un processus ponctuel.

Les processus ponctuels sont des objets très étudiés en probabilité et en statistique pour représenter et analyser des données spatialisées qui interviennent dans une multitude de domaines telle que l'écologie, l'astronomie, l'épidémiologie, la géographie, la sismologie, les télécommunications, la science des matériaux et beaucoup d'autres.

Le cas particulier des processus ponctuels sur la droite réelle est très étudié, la connaissance de la distance entre deux points consécutifs caractérisant le processus. Ce type de processus ponctuel est très utilisé pour modéliser des événements aléatoires dans le temps, tels que l'arrivée d'un client (théorie des files d'attente), l'impulsion d'un neurone...

Théorie des processus ponctuels

En mathématiques, un processus ponctuel est un élément aléatoire dont les valeurs sont des motifs de points, c'est-à-dire des « collections » de points sur un ensemble S {\displaystyle S} .

Il est possible de généraliser en définissant un motif de points comme étant une mesure de comptage localement finie.

Définition

Soit S {\displaystyle S} un espace métrique localement compact équipé de sa tribu borélienne B ( S ) {\displaystyle {\mathcal {B}}(S)} . On note N S {\displaystyle N_{S}} l'ensemble des motifs de points de S {\displaystyle S} , c'est-à-dire l'ensemble des sous-ensembles localement finis de S {\displaystyle S} . Un élément de N S {\displaystyle N_{S}} sera appelé "configuration" et sera noté ω {\displaystyle \omega } .

On munit N S {\displaystyle N_{S}} de la tribu N S {\displaystyle {\mathcal {N}}_{S}} [1],[2],[3] engendrée par les applications de comptage f B {\displaystyle f_{B}}  : N S → N ,   ω ↦ # ( ω ∩ B ) {\displaystyle N_{S}\to \mathbb {N} ,\ \omega \mapsto \#(\omega \cap B)} , où B est un compact de S {\displaystyle S} et où # {\displaystyle \#} désigne le cardinal de l'ensemble fini considéré.

Un processus ponctuel est alors une application mesurable X {\displaystyle X} d'un espace de probabilité vers l'espace mesuré ( N S , N S ) {\displaystyle (N_{S},{\mathcal {N}}_{S})} .

L'exemple le plus commun d'espace S {\displaystyle S} est l'espace euclidien R d {\displaystyle \mathbb {R} ^{d}} ou un de ses sous-espaces. Mais les processus ponctuels ne sont pas limités à ces exemples.

Un cas particulier des processus ponctuels est celui des processus ponctuels définis sur la droite réelle R {\displaystyle \mathbb {R} } (ou la demi-droite réelle R + {\displaystyle \mathbb {R} ^{+}} ). Dans les applications concrètes, cela représente souvent l'occurrence d'événements dans le temps. Pour donner quelques exemples, un processus ponctuel dans le temps peut modéliser les temps d'arrivée de visiteurs dans un musée (avec le processus de Poisson par exemple), la durée avant déclenchement d'une maladie chez une personne (processus de Cox) ou encore les temps auxquels on observe des influx nerveux dans les neurones (processus de Hawkes).

Mesure intensité

La mesure intensité du processus X {\displaystyle X} est une mesure sur S {\displaystyle S} qui mesure le nombre moyen de points du processus qui tombe dans un borélien de S {\displaystyle S} , et s'écrit pour B ∈ S {\displaystyle B\in {\mathcal {S}}} , m X ( B ) := E [ # ( X ∩ B ) ] {\displaystyle m_{X}(B):=\mathbb {E} [\#(X\cap B)]} .

Intensité d'un processus ponctuel

Dans le cas où on étudie des processus ponctuels sur R {\displaystyle \mathbb {R} } (ou R + {\displaystyle \mathbb {R} ^{+}} ), on peut proposer une autre façon intuitive de mesurer l'intensité d'un processus ponctuel : cette mesure est appelée l'intensité du processus ponctuel λ {\displaystyle \lambda } et est définie comme[4] :

λ = l i m h → 0 P r { N ( 0 , h ] > 0 } h {\displaystyle \lambda =lim_{h\rightarrow 0}{\frac {\mathrm {Pr} \{N(0,h]>0\}}{h}}}

D'après le théorème de Khinchin[4], cette limite existe si le processus ponctuel est stationnaire (mais elle peut être infinie). Intuitivement, l'intensité représente la probabilité qu'il y ait au moins une occurrence dans l'intervalle ] x ; x + h ] {\displaystyle ]x;x+h]} quand h {\displaystyle h} tend vers zéro.

Fonctionnelle de Laplace

La fonctionnelle de Laplace[3] d'un processus ponctuel X {\displaystyle X} , noté Ψ X {\displaystyle \Psi _{X}} , est une fonctionnelle de l'ensemble de toutes les fonctions f {\displaystyle f} positives de S {\displaystyle S} dans R {\displaystyle \mathbb {R} } et est définie comme suit:

Ψ X ( f ) = E [ exp ⁡ ( − ∑ x ∈ X f ( x ) ) ] {\displaystyle \Psi _{X}(f)=\mathbb {E} \left[\exp \left(-{\underset {x\in X}{\sum }}f(x)\right)\right]}

Cette fonctionnelle joue un rôle similaire à la fonction caractéristique d'une variable aléatoire. En effet la fonctionnelle de Laplace caractérise la loi d'un processus ponctuel, c'est-à-dire que deux processus ponctuels qui ont des fonctionnelles de Laplace égales ont la même loi.

Théorème de Rényi : Caractérisation par les probabilités de vide

Compte tenu de la structure de la tribu sur N S {\displaystyle {\mathcal {N}}_{S}} , la loi d'un processus ponctuel X {\displaystyle X} est entièrement déterminée par les probabilités ( P ( # ( X ∩ B ) = k ) ) k , B {\displaystyle (\mathbb {P} (\#(X\cap B)=k))_{k,B}} où k {\displaystyle k} parcourt l'ensemble des entiers naturels N {\displaystyle \mathbb {N} } et B {\displaystyle B} l'ensemble des boréliens bornés de S {\displaystyle S} . Mais le théorème de Rényi nous donne une caractérisation beaucoup plus simple.

Théorème de Rényi —  Si l'espace S {\displaystyle S} est séparable complet, alors la loi d'un processus ponctuel est entièrement déterminée par les probabilités de vide (void probabilities en anglais), c'est-à-dire par la famille ( P ( X ∩ B = ∅ ) ) B {\displaystyle (\mathbb {P} (X\cap B=\emptyset ))_{B}} , où B {\displaystyle B} parcours l'ensemble des boréliens bornés.

Processus ponctuel de Poisson

Le processus ponctuel de Poisson est le plus simple et le plus universel des processus ponctuels. C'est une généralisation spatiale du processus de Poisson utilisé en théorie des files d'attente.

Définition d'un processus ponctuel de Poisson —  Soit m {\displaystyle m} une mesure non atomique sur S {\displaystyle S} . Un processus ponctuel X {\displaystyle X} est un processus ponctuel de Poisson de mesure d'intensité m {\displaystyle m} si, pour toutes familles B 1 , … , B n {\displaystyle B_{1},\dots ,B_{n}} de boréliens bornés disjoints et pour tous entiers naturels k 1 , … , k n {\displaystyle k_{1},\dots ,k_{n}} ,

P ( # ( X ∩ B i ) = k i , 1 ≤ i ≤ n ) = ∏ i = 1 n exp ⁡ ( − m ( B i ) ) m ( B i ) k i k i ! {\displaystyle \mathbb {P} (\#(X\cap B_{i})=k_{i},1\leq i\leq n)=\prod _{i=1}^{n}\exp(-m(B_{i})){\frac {m(B_{i})^{k_{i}}}{k_{i}!}}}

Propriétés des processus ponctuels de Poisson

Cette section regroupe les propriétés fondamentales des processus ponctuels de Poisson. Ces résultats sont souvent la conséquence du théorème de Rényi.

Proposition (Superposition de deux processus ponctuels de Poisson)[1],[3] —  Soient X {\displaystyle X} et Y {\displaystyle Y} deux processus ponctuels de Poisson de mesures d'intensité m X {\displaystyle m_{X}} et m Y {\displaystyle m_{Y}} . Alors la superposition X ∪ Y {\displaystyle X\cup Y} des deux processus est un processus ponctuel de Poisson de mesure d'intensité m X + m Y {\displaystyle m_{X}+m_{Y}} .

Proposition (Amincissement (thinning) d'un processus ponctuel de Poisson)[1],[3] —  Soient X {\displaystyle X} un processus ponctuel de Poisson de mesure d'intensité m X {\displaystyle m_{X}} et p : S → [ 0 , 1 ] {\displaystyle p:S\to [0,1]} une fonction mesurable. Nous construisons le processus X p {\displaystyle X_{p}} en décidant pour chaque point x {\displaystyle x} du processus X {\displaystyle X} , et de manière indépendante, de la garder avec probabilité p ( x ) {\displaystyle p(x)} et de l'effacer avec probabilité 1 − p ( x ) {\displaystyle 1-p(x)} .

Alors le processus X p {\displaystyle X_{p}} est un processus ponctuel de Poisson de mesure d'intensité m p ( . ) = ∫ . p ( x ) m ( d x ) {\displaystyle m_{p}(.)=\int _{.}p(x)m(dx)} .

Proposition (Loi du processus conditionné par le nombre de points)[1],[3] —  Soit X {\displaystyle X} un processus ponctuel de Poisson d'intensité m {\displaystyle m} et soit B {\displaystyle B} un borélien borné de S {\displaystyle S} . Alors conditionnellement à l'événement # ( X ∩ B ) = n {\displaystyle \#(X\cap B)=n} , les n {\displaystyle n} points du processus sont des réalisations indépendantes et identiquement distribuées de loi m ( . ∩ B ) m ( B ) {\displaystyle {\frac {m(.\cap B)}{m(B)}}} .

Simulation d'un processus ponctuel de Poisson

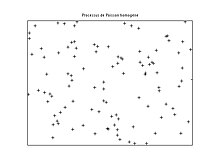
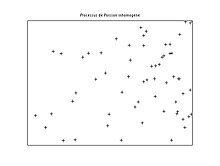
m ( d x , d y ) = 100 d x d y {\displaystyle m(dx,dy)=100dxdy} , fenêtre [ 0 , 1 ] 2 {\displaystyle [0,1]^{2}}
m ( d x , d y ) = 100 x d x d y {\displaystyle m(dx,dy)=100xdxdy} , fenêtre [ 0 , 1 ] 2 {\displaystyle [0,1]^{2}}

La dernière proposition fournit une méthode simple et très efficace pour simuler des processus ponctuels de Poisson.

Pour simuler un processus ponctuel de Poisson d'intensité m {\displaystyle m} dans un compact B {\displaystyle B} [1],[3] :

  • Déterminer le nombre de points. Pour ce faire on simule une loi de Poisson n {\displaystyle n} de moyenne m ( B ) {\displaystyle m(B)} .
  • Déterminer la position des n {\displaystyle n} points. Pour cela, on simule n {\displaystyle n} variables aléatoires i.i.d. de loi m {\displaystyle m} restreinte sur B {\displaystyle B} .

L'objet simulé est une réalisation du processus ponctuel de Poisson sur la fenêtre B {\displaystyle B} de mesure d'intensité m {\displaystyle m} .

Formule de Slivnyak-Mecke

La formule de Slivnyak-Mecke[5],[6], aussi connue sous le nom de formule de Campbell, est une formule très utilisée en géométrie stochastique et en physique statistique.

Théorème —  Soit F : S × N S → R + {\displaystyle F:S\times N_{S}\to \mathbb {R} ^{+}} une fonction mesurable et X {\displaystyle X} un processus ponctuel de Poisson d'intensité m {\displaystyle m} . Alors nous avons

E [ ∑ x ∈ X F ( x , X ∖ x ) ] = E [ ∫ S F ( x , X ) m ( d x ) ] . {\displaystyle \mathbb {E} \left[\sum _{x\in X}F(x,X\setminus x)\right]=\mathbb {E} \left[\int _{S}F(x,X)m(dx)\right].}

Le terme de droite est dans de nombreux cas calculable et permet de calculer en moyenne, grâce à la formule de Slivnyak-Mecke, la somme des contributions de chaque point du processus.

Processus de Hawkes

Le processus ponctuel de Hawkes (ou processus auto-excité) est un processus ponctuel pour lequel les réalisations futures dépendent des réalisations passées. Cette caractéristique le différencie des processus ponctuels de Poisson pour lesquels l'indépendance entre deux événements est une propriété fondamentale.

Le processus de Hawkes a été formalisé pour la première fois par Alan G. Hawkes en 1971[7], sous le nom de processus auto-excité. Ce processus a d'abord été utilisé en sismologie[8] pour modéliser la survenue de répliques suites à un séisme. Depuis, de nombreuses variantes du processus ont été développées et utilisées dans divers domaines, par exemple en sociologie pour étudier la diffusion des mèmes sur les réseaux sociaux[9], en épidémiologie pour modéliser la diffusion d'une maladie[10] ou encore en neurosciences pour modéliser les influx nerveux dans les neurones[11].

Processus de Hawkes univarié

Dans l'article fondateur de Alan G. Hawkes[7], le processus auto-excité est défini à partir de son intensité au temps t {\textstyle t} , notée λ ( t ) {\textstyle \lambda (t)} . L'intensité d'un processus ponctuel est une mesure du taux instantané d'occurrence d'événements. Dans le cas du processus de Hawkes, l'intensité λ ( t ) {\textstyle \lambda (t)} s'écrit :

λ ( t ) = ν + ∫ − ∞ t g ( t − u ) d N ( u ) {\displaystyle \lambda (t)=\nu +\int _{-\infty }^{t}g(t-u)\mathrm {d} N(u)}

Dans cette formule, l'intensité est formée de deux composantes : le scalaire ν {\textstyle \nu } qui représente le taux d'occurrence spontané (qui n'est pas dû aux événements antérieurs) et l'intégrale entre − ∞ {\textstyle -\infty } et t {\textstyle t} , qui désigne la dépendance aux temps antérieurs. Ainsi, l'intensité au temps t {\textstyle t} dépend du nombre d'événements qui sont survenus au temps u {\textstyle u} (antérieur à t {\displaystyle t} ) N ( u ) {\displaystyle N(u)} .

L'influence de N ( u ) {\displaystyle N(u)} sur λ ( t ) {\textstyle \lambda (t)} est décrite par la fonction g {\displaystyle g} , appelée noyau. Le noyau décrit la façon dont l'excitation évolue en fonction du délai t − u {\displaystyle t-u} entre un événement passé (survenu au temps u {\textstyle u} ) et le temps t {\textstyle t} . Cette fonction doit tendre vers zéro quand l'intervalle de temps est grand (l'excitation s'atténue) et elle doit prendre des valeurs positives uniquement. Cependant, des extensions du processus de Hawkes ont été proposées dans lesquelles g {\displaystyle g} peut prendre des valeurs négatives, et ainsi modéliser une auto-inhibition. Une paramétrisation simple de g {\displaystyle g} est l'exponentielle décroissante, par exemple de la forme g ( t − u ) = a e − a ( t − u ) {\displaystyle g(t-u)=ae^{-a(t-u)}} (avec a {\displaystyle a} un paramètre de la fonction, scalaire).

Processus de Hawkes multivarié

Les processus de Hawkes ont également été généralisés au cas multivarié[3] : c'est-à-dire que plusieurs éléments (dimensions) s'excitent mutuellement. Par exemple, il peut s'agir de plusieurs neurones qui vont se transmettre des influx nerveux les uns aux autres. Dans le cas multivarié, l'équation du processus de Hawkes devient :

λ i ( t ) = ν i + ∑ j = 1 N ∫ − ∞ t g j → i ( t − u ) d N j ( u ) {\displaystyle \lambda _{i}(t)=\nu _{i}+\sum _{j=1}^{N}\int _{-\infty }^{t}g_{j\rightarrow i}(t-u)\mathrm {d} N_{j}(u)}

L'indice i {\displaystyle i} ( 1 ≤ i ≤ N {\displaystyle 1\leq i\leq N} ) signifie qu'on s'intéresse à la dimension i {\displaystyle i} (neurone i {\displaystyle i} par exemple). Comme dans le cas univarié, ν i {\textstyle \nu _{i}} représente le taux d'occurrence spontané (qui peut être différent pour chaque dimension i {\displaystyle i} ). L'intégrale entre − ∞ {\textstyle -\infty } et t {\textstyle t} décrit l'influence de l'histoire du processus : pour la dimension i {\displaystyle i} , on va sommer les influences des N {\displaystyle N} dimensions, et le noyau g j → i {\displaystyle g_{j\rightarrow i}} décrit l'influence du neurone j {\displaystyle j} ( 1 ≤ j ≤ N {\displaystyle 1\leq j\leq N} ) sur le neurone i {\displaystyle i} . On intègre la fonction g j → i {\displaystyle g_{j\rightarrow i}} sur d N j ( u ) {\displaystyle \mathrm {d} N_{j}(u)} , qui est le nombre d'événements survenus au temps u {\textstyle u} dans la dimension j {\displaystyle j} . Dans le cas où j = i {\displaystyle j=i} , g i → i {\displaystyle g_{i\rightarrow i}} décrit l'auto-excitation de la dimension i {\displaystyle i} sur elle-même.

Dans le cas où on observe un processus de Hawkes, mais qu'on ne connaît pas les g j → i {\displaystyle g_{j\rightarrow i}} , la question d'intérêt est souvent de déterminer quelles fonctions g j → i {\displaystyle g_{j\rightarrow i}} sont non-nulles. En effet, si g j → i {\displaystyle g_{j\rightarrow i}} est différente de zéro, cela signifie que la dimension j {\displaystyle j} excite la dimension i {\displaystyle i} . Par exemple, dans le cas où on observe des neurones, une fonction g j → i {\displaystyle g_{j\rightarrow i}} non nulle peut signifier que le neurone j {\displaystyle j} est connecté au neurone i {\displaystyle i} .

Autres développements

De nombreuses généralisations du processus de Hawkes ont été proposées : pour prendre en compte l'auto-inhibition, dans le cas spatio-temporel, avec des noyaux non-paramétriques ou encore avec une intensité log-linéaire. De nombreux algorithmes d'inférence ont aussi été proposés afin de déterminer les paramètres (inconnus) d'un processus de Hawkes à partir d'une de ses réalisations.

Notes et références

  1. ↑ a b c d et e Chiu, Sung Nok., Kendall, W. S. et Mecke, Joseph., Stochastic geometry and its applications., , 544 p. (ISBN 978-0-470-66481-0, OCLC 843455184, lire en ligne)
  2. ↑ Matthes, Klaus, et Mecke, Joseph,, Infinitely divisible point processes, Wiley, (ISBN 978-0-471-99460-2)
  3. ↑ a b c d e f et g Daley et Vere-Jones 2007
  4. ↑ a et b (en) « Simple Results for Stationary Point Processes on the Line », dans An Introduction to the Theory of Point Processes: Volume I: Elementary Theory and Methods, Springer, coll. « Probability and its Applications », (ISBN 978-0-387-21564-8, DOI 10.1007/0-387-21564-6_3, lire en ligne), p. 41–65
  5. ↑ (en) Schneider, Rolf., Stochastic and integral geometry, Berlin, Springer, (ISBN 978-3-540-78859-1, OCLC 271648052, lire en ligne)
  6. ↑ (en) Kallenberg, Olav., Random measures, Berlin/London/Orlando/San Diego etc., Akademie-Verlag, , 187 p. (ISBN 0-12-394960-2, OCLC 16646248, lire en ligne)
  7. ↑ a et b ALAN G. HAWKES, « Spectra of some self-exciting and mutually exciting point processes », Biometrika, vol. 58, no 1,‎ , p. 83–90 (ISSN 0006-3444, DOI 10.1093/biomet/58.1.83, lire en ligne, consulté le )
  8. ↑ (en) Yosihiko Ogata, « Space-Time Point-Process Models for Earthquake Occurrences », Annals of the Institute of Statistical Mathematics, vol. 50, no 2,‎ , p. 379–402 (ISSN 1572-9052, DOI 10.1023/A:1003403601725, lire en ligne, consulté le )
  9. ↑ Chuan Luo, Xiaolong Zheng et Daniel Zeng, « Inferring social influence and meme interaction with Hawkes processes », 2015 IEEE International Conference on Intelligence and Security Informatics (ISI),‎ , p. 135–137 (DOI 10.1109/ISI.2015.7165953, lire en ligne, consulté le )
  10. ↑ (en) Wen-Hao Chiang, Xueying Liu et George Mohler, « Hawkes process modeling of COVID-19 with mobility leading indicators and spatial covariates », International Journal of Forecasting,‎ (ISSN 0169-2070, DOI 10.1016/j.ijforecast.2021.07.001, lire en ligne, consulté le )
  11. ↑ (en) Régis C. Lambert, Christine Tuleau-Malot, Thomas Bessaih et Vincent Rivoirard, « Reconstructing the functional connectivity of multiple spike trains using Hawkes models », Journal of Neuroscience Methods, vol. 297,‎ , p. 9–21 (DOI 10.1016/j.jneumeth.2017.12.026, lire en ligne, consulté le )

Bibliographie

  • (en) Daryl J Daley et David Vere-Jones, An introduction to the theory of point processes : general theory and structure, vol. II, Springer Science and Business Media, (1re éd. 1988)

Articles connexes

  • icône décorative Portail des probabilités et de la statistique