Moyenne harmonique

Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus.
Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus.

Cet article ne cite pas suffisamment ses sources ().

Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualité traitant du thème abordé ici, merci de compléter l'article en donnant les références utiles à sa vérifiabilité et en les liant à la section « Notes et références ».

En pratique : Quelles sources sont attendues ? Comment ajouter mes sources ?

La moyenne harmonique H de nombres réels strictement positifs a1, ..., an est définie par :

H = n 1 a 1 + 1 a 2 + ⋯ + 1 a n ⋅ {\displaystyle H={\frac {n}{{\dfrac {1}{a_{1}}}+{\dfrac {1}{a_{2}}}+\cdots +{\dfrac {1}{a_{n}}}}}\cdot }

C'est l'inverse de la moyenne arithmétique des inverses des termes. La moyenne harmonique est donc utilisée lorsqu'on veut déterminer un rapport moyen, dans un domaine où il existe des liens de proportionnalité inverses.

Exemples

Dans certains cas, la moyenne harmonique donne la véritable notion de « moyenne ». Par exemple, si pour la moitié de la distance d'un trajet vous voyagez à 40 kilomètres par heure, et que pour l'autre moitié vous voyagez à 60 kilomètres par heure, votre vitesse moyenne est alors donnée par la moyenne harmonique de 40 km/h et 60 km/h, ce qui donne 48 km/h. Votre temps de voyage total est donc le même que si vous aviez voyagé à 48 kilomètres par heure sur l'ensemble de la distance (attention toutefois, si vous aviez voyagé la moitié du temps à une vitesse, et l'autre moitié du temps (et non de la distance) à une autre vitesse, la moyenne arithmétique, dans ce cas 50 kilomètres par heure, vous aurait donné la bonne moyenne).

De même, si un circuit électrique a deux résistances reliées en parallèle, la première faisant 40 Ω et l'autre 60 Ω, la résistance moyenne des deux est 48 Ω ; la résistance totale du circuit est la même que si les deux résistances en parallèle étaient remplacées par deux résistances de 48 Ω (attention, cette résistance moyenne n'est pas la résistance équivalente qui est, elle, de 24 Ω, et qui correspond à remplacer les deux résistances en parallèle par une seule résistance de 24 Ω).

Un autre exemple utile est celui de l'usure des pneus d'un véhicule entre l'avant et l'arrière. Si votre train de pneus avant est usé au bout de 50000 km tandis que celui arrière l'est au bout de 35000 km vous pouvez connaitre le kilométrage au bout duquel permuter les roues avants et arrières en prenant la moitié de la moyenne harmonique. Soit ici : 35000 × 50000 35000 + 50000 = 20588 {\displaystyle {\frac {35000\times 50000}{35000+50000}}=20588} .

Moyenne harmonique de deux nombres

Formule

La moyenne harmonique de deux réels strictement positifs a  et  b {\displaystyle a{\text{ et }}b} s'écrit :

H = 2 1 / a + 1 / b = 2 a b a + b ⋅ {\displaystyle H={\frac {2}{1/a+1/b}}={\frac {2ab}{a+b}}\cdot }

Par exemple, chaque terme de la série harmonique ∑ 1 n {\textstyle \sum {1 \over n}} est la moyenne harmonique des termes précédent et suivant.

Lien avec les moyennes géométrique et arithmétique

Cette moyenne est aussi reliée à la moyenne arithmétique,

A = a + b 2 , {\displaystyle A={\frac {a+b}{2}},}

et à la moyenne géométrique,

G = a b , {\displaystyle G={\sqrt {ab}},}

par la formule suivante :

H = G 2 A ⋅ {\displaystyle H={\frac {G^{2}}{A}}\cdot }

d'où

G = A H {\displaystyle G={\sqrt {AH}}} , c.-à-d. que la moyenne géométrique est la racine carrée de la moyenne arithmétique multipliée par la moyenne harmonique.

Proportions harmonique et contre-harmonique

Trois réels strictement positifs a < b < c {\displaystyle a<b<c} sont dits "en proportion harmonique" si le rapport du deuxième écart au premier écart est égal au rapport du troisième nombre au premier, autrement dit si c − b b − a = c a {\displaystyle {\frac {c-b}{b-a}}={\frac {c}{a}}}  ; cela équivaut à ce que b = 2 a c a + c {\displaystyle b={\frac {2ac}{a+c}}} , autrement dit à ce que le nombre central soit la moyenne harmonique des deux autres.

Ces nombres sont dits « en proportion contre-harmonique » si les rapports sont inversés, autrement dit si b − a c − b = c a {\displaystyle {\frac {b-a}{c-b}}={\frac {c}{a}}}  ; cela équivaut à ce que b = a 2 + c 2 a + c {\displaystyle b={\frac {a^{2}+c^{2}}{a+c}}} , qui est appelé la moyenne "contre-harmonique" de a  et  c {\displaystyle a{\text{ et }}c} .

Par exemple, 2, 3 et 6 sont en proportion harmonique, tandis que 2, 5, et 6 sont en proportion contre-harmonique.

Lien avec la division harmonique

Les réels strictement positifs a < b < c {\displaystyle a<b<c} sont en proportion harmonique si et seulement si les quatre nombres 0 , b , a , c {\displaystyle 0,b,a,c} forment une division harmonique, autrement dit si le birapport ( 0 , b , a , c ) = a − b a : c − b c {\displaystyle (0,b,a,c)={\frac {a-b}{a}}:{\frac {c-b}{c}}} est égal à -1.

Inversement, quatre points A , B , C , D {\displaystyle A,B,C,D} d'une droite orientée forment une division harmonique si et seulement si A B ¯ {\displaystyle {\overline {AB}}} est la moyenne harmonique de A C ¯ {\displaystyle {\overline {AC}}} et A D ¯ {\displaystyle {\overline {AD}}} , ce que l'on écrit sous la forme de la relation de Descartes : 2 A B ¯ = 1 A C ¯ + 1 A D ¯ . {\displaystyle {\frac {2}{\overline {AB}}}={\frac {1}{\overline {AC}}}+{\frac {1}{\overline {AD}}}.}

Constructions géométriques

A: moyenne arithmétique des nombres a et b, G moyenne géométrique, H harmonique, Q quadratique.

À partir d'un demi-disque

La moyenne harmonique fait partie des moyennes pythagoriciennes et peut être construite[1].

On considère un segment [AB], séparé en deux segments de longueurs a et b en K. Le demi-cercle de diamètre [AB], centré en O, a donc un rayon égal à la moyenne arithmétique de a  et  b {\displaystyle a{\text{ et }}b} , et la perpendiculaire au diamètre issue de K, qui intercepte le demi-cercle en M, a une longueur égale à la moyenne géométrique (c'est le théorème de la moyenne géométrique). On trace alors le rayon [OM] du demi-cercle, puis la hauteur [KP] du triangle OMK. Comme tous les triangles formés sont semblables, on a :

K M O M = P M K M ⟺ a b a + b 2 = P M a b ⟺ P M = 2 a b a + b {\displaystyle {\frac {KM}{OM}}={\frac {PM}{KM}}\Longleftrightarrow {\frac {\sqrt {ab}}{\frac {a+b}{2}}}={\frac {PM}{\sqrt {ab}}}\Longleftrightarrow PM={\frac {2ab}{a+b}}}

qui est bien égale à la moyenne harmonique de a  et  b {\displaystyle a{\text{ et }}b} .

À partir d'un trapèze

Dans un trapèze convexe de bases de longueurs a  et  b {\displaystyle a{\text{ et }}b} , le segment parallèle aux bases joignant les deux côtés et passant par le point d'intersection des diagonales a pour longueur la moyenne harmonique de a  et  b {\displaystyle a{\text{ et }}b} , ceci quelles que soient les longueurs des côtés.

Plus précisément, avec les notations de la figure ci-contre, on a I J = I K = a b a + b {\displaystyle IJ=IK={\frac {ab}{a+b}}} .

Démonstration

D'après le théorème de Thales dans le triangle A B C {\displaystyle ABC} , on a a I J = C B C I = 1 + I B I C {\displaystyle {\frac {a}{IJ}}={\frac {CB}{CI}}=1+{\frac {IB}{IC}}} .

Or dans le trapèze croisé A B C D {\displaystyle ABCD} , on a a b = I B I C {\displaystyle {\frac {a}{b}}={\frac {IB}{IC}}} , d'où a I J = 1 + a b {\displaystyle {\frac {a}{IJ}}=1+{\frac {a}{b}}} , et I J = a b a + b {\displaystyle IJ={\frac {ab}{a+b}}} .

Idem pour I K {\displaystyle IK} .

Ce résultat est utilisé dans la résolution du problème des deux échelles.

Constructions de la moitié de la moyenne harmonique

Il existe plusieurs constructions donnant la moitié de la moyenne harmonique de deux nombres, illustrées dans les figures suivantes :

  • Problème de deux échelles
    Problème de deux échelles
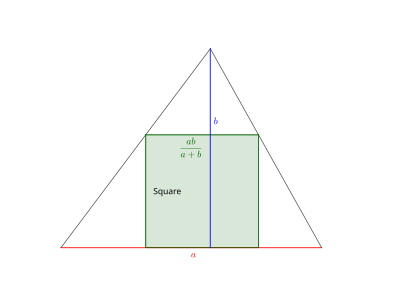  • Dans un triangle de base a et de hauteur b, le côté du carré inscrit est de longueur ab/(a+b)
    Dans un triangle de base a et de hauteur b, le côté du carré inscrit est de longueur ab/(a+b)
  • Dans un triangle tel qu'un angle entre deux côtés de longueurs a et b mesure 120°, la longueur de la bissectrice est de ab/(a+b)
    Dans un triangle tel qu'un angle entre deux côtés de longueurs a et b mesure 120°, la longueur de la bissectrice est de ab/(a+b)

Applications

  • en dimensionnement mécanique, pour calculer le rayon équivalent, de rayons de courbure, lors du contact entre deux sphères ou deux cylindres, d'après la loi de Hertz-Boussinesq (voir aussi « Contact de Hertz ») ;
  • en apprentissage automatique, la F-mesure F 1 {\displaystyle F_{1}} associée à un modèle d'apprentissage est la moyenne harmonique de ses précision et rappel.
  • en finance, pour le calcul d'un multiple de valorisation moyen d'un portefeuille de titres (ex : calcul du ratio PE moyen d'un portefeuille d'actions)

Voir aussi

Références

  1. ↑ (en) Howard Eves, « Means Appearing in Geometric Figures », Mathematics Magazine,‎ (lire en ligne)
  • icône décorative Portail des mathématiques