Fermin–Diracin statistiikka
Fermin–Diracin statistiikka on statistisessa fysiikassa jakaumalaki, joka kuvaa identtisten, heikosti vuorovaikuttavien fermionien energiajakaumaa termodynaamisessa tasapainotilassa. Fermionit ovat alkeishiukkasia, jotka noudattavat Paulin kieltosääntöä ja joita tämän vuoksi voi olla vain yksi samalla yksihiukkastilalla toisin kuin bosoneja, joita tämä rajoitus ei koske. Fermioneja ovat esimerkiksi protonit, neutronit ja elektronit.
Paulin kieltosäännön esitti Wolfgang Pauli vuonna 1925. Sen perusteella Enrico Fermi ja Paul Dirac johtivat seuraavana vuonna toisistaan riippumatta Fermin–Diracin jakaumalain.
Eri statistiikkojen vertailua
Statistisessa fysiikassa käytetään kolmea erilaista jakaumaa, jotka ovat:
- Maxwellin-Boltzmannin statistiikka
- Bosen-Einsteinin statistiikka
- Fermin–Diracin statistiikka
Maxwellin–Bolzmannin statistiikkaa sovelletaan molekyyleihin klassisessa termodynamiikassa. Kvanttiteoria on kuitenkin osoittanut, ettei se sovellu minkään alkeishiukkasen energiajakauman kuvaamiseen muutoin kuin tietyissä tapauksissa likimääräisesti.
Bosen–Einsteinin statistiikka soveltuu bosoneille kuten fotoneille ja mesoneille. Fermin–Diracin statistiikka soveltuu fermioneille kuten elektroneille ja protoneille, joita Paulin kieltosäännön mukaan ei voi olla useampi kuin yksi samassa kvanttitilassa.
Sekä Maxwellin-Boltzmannin että Bosen-Einsteinin statistiikassa oletetaan, että jokaisessa energiatilassa voi olla rajoittamaton määrä hiukkasia. Bosen-Einsteinin statistiikassa oletetaan kuitenkin, toisin kuin klassisessa Maxwellin-Boltzmannin statistiikassa, ettei hiukkasia periaatteessakaan voida yksilöidä, minkä vuoksi jakaumalakia johdettaessa symmetriset alkeistapaukset muodostetaan eri tavoin. Sitä vastoin Fermin-Diracin statistiikassa otetaan huomioon, että kullakin kvanttitilalla voi samanaikaisesti olla enintään yksi hiukkanen.
Jakaumalaki
Kun sekä hiukkasten että energiatilojen lukumäärä ovat suuria lukuja, hiukkasten todennäköinen lukumäärä energiatilassa i on Fermin–Diracin statistiikassa:
missä ja:
- ni on tilassa i olevien hiukkasten lukumäärä
- gi on tilan i degeneraatio
- εi on tilan i energia
- μ on kemiallinen potentiaali
- k on Boltzmannin vakio
- T on absoluuttinen lämpötila
Energiatilan degeneraatiolla tarkoitetaan niiden kvanttitilojen lukumäärää, joissa hiukkasella on tietty määrä energiaa. Paulin kieltosäännöstä seuraa, että tämä on samalla suurin määrä hiukkasia, joilla voi samanaikaisesti olla tietty määrä energiaa.
Jos on paljon pienempi kuin , tämä voidaan pyöristää muotoon
- ,
mikä on sama kuin Maxwellin–Boltzmannin jakaumalaki.
- Fermin-Diracin jakauma
-
![Eri energiatilojen täyttöaste. Korkeammassa lämpötilassa T käyrä on loivempi, ja '"`UNIQ--postMath-00000006-QINU`"'=0.5 kun '"`UNIQ--postMath-00000007-QINU`"' = '"`UNIQ--postMath-00000008-QINU`"'. Vaikka kaaviosta ei käy ilmi, '"`UNIQ--postMath-00000009-QINU`"' alenee lämpötilan T noustessa T.[1]](//upload.wikimedia.org/wikipedia/commons/thumb/1/15/FD_e_mu.jpg/200px-FD_e_mu.jpg) Eri energiatilojen täyttöaste. Korkeammassa lämpötilassa T käyrä on loivempi, ja =0.5 kun = .
Eri energiatilojen täyttöaste. Korkeammassa lämpötilassa T käyrä on loivempi, ja =0.5 kun = .
Vaikka kaaviosta ei käy ilmi, alenee lämpötilan T noustessa T.[1] -
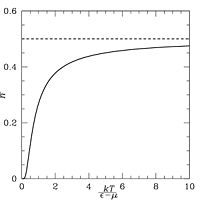
Energian riippuvuus lämpötilasta T.
Fermin–Diracin jakaumalain johtaminen
Oletetaan, että on olemassa joukko energiatasoja, jotka on merkitty indeksinumeroilla . Kunkin energiatilan energia on , ja siinä on hiukkasta. Oletetaan edelleen, että kukin tila jakautuu vielä erilliseen alatasoon, joista jokaisella on yhtä suuri energia mutta jotka jollakin muulla tavalla eroavat toisistaan. Näillä eri alatasoilla olevilla hiukkasilla voi esimerkiksi olla eri suuri liikemäärä mutta sama määrä energiaa. Tasoon liittyvien tilojen lukumäärää sanotaan tämän energiatason "degeneraatioksi". Kullakin tällaisella alatasolla voi olla vain yksi hiukkanen.
Olkoon niiden tapojen lukumäärä, joilla hiukkasta voidaan sijoittaa näille yhteensä energiatason alatasolle. Kun hiukkasia voi olla vain yksi kullakin alatasolla, tällaisia tapoja on yhtä monta kuin g-alkioisella joukolla in n-alkoisia osajoukkoja eli
Niinpä niiden tapojen lukumäärä, joilla hiukkaset voivat jakautua eri energiatasojen kesken, saadaan kertomalla eri energiatasoja vastaavat lukumäärät keskenään:
kun oletetaan, että .
Systeemi on termodynaamisessa tasapainotilassa, kun W:llä on suurin mahdollinen arvo. Tämä vastaa jakaumaa, jonka todennäköisyys on suurin. Jos oletetaan, että hiukkasten kokonaismäärä ja yhteenlaskettu energia tunnetaan, suureet ja saavat maksiminsa samalla :n arvolla, joista se on matemaattisesti helpompi johtaa jälkimmäiselle. Voidaan rajoittua ratkaisuihin, jotka saadaan Lagrangen kertoimien avulla:
Jos oletetaan, että on hyvin suuri luku, voidaan kertomalle laskea likiarvo Stirlingin kaavalla:
,
jolloin saadaan
Tämän maksimi saadaan ottamalla siitä derivaatta :n suhteen ja etsimällä derivaatalle nollakohta. Tällöin saadaan Fermin–Diracin statistiikan mukainen lukumäärä:
Termodynamiikan avulla voidaan osoittaa, että tässä kaavassa esiintyvät parametrit ja vastaavat systeemiin liittyviä fysikaalisia suureita seuraavasti:
ja
,
missä on Boltzmannin vakio, absoluuttinen lämpötila ja systeemin kemiallinen potentiaali. Näin ollen kaava voidaan lopulta kirjoittaa muotoon
Katso myös
Lähteet
- Annett, James F. (2004). Superconductivity, Superfluids and Condensates. New York: Oxford University Press. ISBN 0198507550.
- Carter, Ashley H. (2001). Classical and Statistical Thermodynamics. Upper Saddle River, NJ: Prentice Hall. ISBN 0137792085.
- Griffiths, David J. (2005). Introduction to Quantum Mechanics, 2nd, Upper Saddle River, NJ: Pearson, Prentice Hall. ISBN 0131911759.
Viitteet
- ↑ Kittel, Charles: Introduction to Solid State Physics (4th Ed.), s. 245, Figs. 4 and 5. John Wiley & Sons, Inc, 1971.





![Eri energiatilojen täyttöaste. Korkeammassa lämpötilassa T käyrä on loivempi, ja '"`UNIQ--postMath-00000006-QINU`"'=0.5 kun '"`UNIQ--postMath-00000007-QINU`"' = '"`UNIQ--postMath-00000008-QINU`"'. Vaikka kaaviosta ei käy ilmi, '"`UNIQ--postMath-00000009-QINU`"' alenee lämpötilan T noustessa T.[1]](http://upload.wikimedia.org/wikipedia/commons/thumb/1/15/FD_e_mu.jpg/200px-FD_e_mu.jpg)








































