Kalkulu multibariable

Aldagai anitzeko kalkulua (kalkulu aldagaianiztuna edo kalkulu multibariablea ere deitzen zaio) aldagai bakar bateko kalkuluaren orokortze bat da, aldagai anitz dituen funtzioak azter ditzaken. Hau da, matematikaren adar hau aldagai anitzdunen funtzioen deribazioa eta integrazioa ahalbidetzen ditu.^[1]

Aldagai anitzeko kalkulua kalkulu aurreratuaren oinarrizko zatitzat har daiteke; halere, ez dira gauza berdinak, kalkulu aurreratua espazio euklideoetan aritzen baita, besteak beste.

Ohiko eragiketak

Limiteak eta jarraitutasuna

Kalkulu aldagaianitzaren bidezko limite eta jarraitutasunaren azterketak emaitza kontraintuitibo asko ematen ditu, aldagai bakarreko funtzioak aztertzean agertzen ez diren arren. Adibidez, bi aldagaiko funtzio eskalar batzuetan, eremuan dauden puntu batzuek limite ezberdinak ematen dituzte bide ezberdinetatik heltzen bada haietara^[1]. Adibidez, funtzio hau

${\displaystyle f(x,y)={\frac {x^{2}y}{x^{4}+y^{2}}}}$

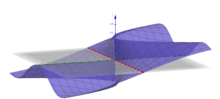
zerora hurbiltzen da ${\displaystyle (0,0)}$ puntua jatorritik doazen lerroen (${\displaystyle y=kx}$) bidez hurbiltzen denean. Hala ere, puntura parabola (${\displaystyle y=\pm x^{2}}$) baten bidez heltzen denean, funtzioaren balioak ${\displaystyle \pm 1/2}$ko limitea du. Puntu berdinak bi emaitza ezberdin ematen dituenez erabilitzen den ibilbidearen arabera, ez da limite orokor bat existitzen puntu honetan-

Aldagaianitz jarraitutasuna betetzeko jarraitasun bakuna ez dela nahikoa abidide honez bidez ere ikus daiteke. ^[1] Bereziki, bi parametro erreal dituen balio errealeko funtzio baten kasuan, ${\displaystyle f(x,y)}$, ${\displaystyle f}$ ${\displaystyle x}$n jarraia izateak ${\displaystyle y}$ konstante mantentzean, baita ${\displaystyle f}$ ${\displaystyle y}$n jarraia izateak ${\displaystyle x}$ konstante mantentzen denean, ez du esan nahi ${\displaystyle f}$ jarraia denik berez.

Imajinatu:

${\displaystyle f(x,y)={\begin{cases}{\frac {y}{x}}-y&{\text{baldin}}\quad 0\leq y<x\leq 1\\{\frac {x}{y}}-x&{\text{baldin}}\quad 0\leq x<y\leq 1\\1-x&{\text{baldin}}\quad 0<x=y\\0&{\text{beste balioetarako}}.\end{cases}}}$

Erraz egiazta daiteke funtzio hori zero dela mugan, definizioz, eta ${\displaystyle (0,1)\times (0,1)}$ laukitik kanpo. Gainera, hurrengo funtzioak definitzen baditugu ${\displaystyle x}$ eta ${\displaystyle y}$ konstanteekin, hala nola ${\displaystyle 0\leq a\leq 1}$:

${\displaystyle g_{a}(x)=f(x,a)\quad }$ eta ${\displaystyle \quad h_{a}(y)=f(a,y)\quad }$

jarraiak direla ikusten dugu. Zehazki,

${\displaystyle g_{0}(x)=f(x,0)=h_{0}(0,y)=f(0,y)=0}$, edozein x edo yrako.

Hala ere, ${\displaystyle f\left({\tfrac {1}{n}},{\tfrac {1}{n}}\right)}$ sekuentziak, ${\displaystyle n}$ arruntentzat, ${\displaystyle \lim _{n\to \infty }f\left({\tfrac {1}{n}},{\tfrac {1}{n}}\right)=1}$ konbergentzia lortzen du, funtzioa etena bihurtuz ${\displaystyle (0,0)}$ puntuan. Jatorrira ${\displaystyle x}$ edo ${\displaystyle y}$ ardatzekiko paraleloak ez diren norabideetatik hurbilduz, eten hori agerrarazten da.

Jarraitutasuna funtzio konposatuetan

${\displaystyle f(x,y)}$ ${\displaystyle (a,b)}$n jarraia izanda, eta ${\displaystyle g}$ ${\displaystyle f(a,b)}$n jarraia den aldagai bakarreko funtziotzat hartuz, ${\displaystyle h=g\circ f}$ funtzio konposatua, ${\displaystyle h(x,y)=g(f(x,y))}$ formularen bidez definituta, jarraia da ${\displaystyle (a,b)}$n.

Adibide nabariak ${\displaystyle \exp(x-y)}$ eta ${\displaystyle \ln(1+xy-4x+10y)}$ dira.

Funtzio jarraituen ezaugarriak

${\displaystyle f(x,y)}$ eta ${\displaystyle g(x,y)}$ biak jarraiak badira ${\displaystyle (a,b)}$n:

${\displaystyle f(x,y)\pm g(x,y)}$ jarraiak dira ${\displaystyle (a,b)}$n.

${\displaystyle cf(x,y)}$ eta ${\displaystyle cg(x,y)}$ jarraituak dira ${\displaystyle (a,b)}$n, edozein c konstanterako.

${\displaystyle f(x,y)}$ ${\displaystyle .}$ ${\displaystyle g(x,y)}$ jarraia da ${\displaystyle (a,b)}$n.

${\displaystyle {\frac {f(x,y)}{g(x,y)}}}$ jarraia da ${\displaystyle (a,b)}$n, baldin ${\displaystyle g(a,b)\neq 0.}$

v) ${\displaystyle \mid f(x,y)\mid }$ edota ${\displaystyle \mid g(x,y)\mid }$ jarraiak dira ${\displaystyle (a,b)}$n.

Deribazio partziala

Deribatu partzialak deribatuarez esanahia dimentsio handiagoetara orokortzen du. Aldagai anitzeko funtzio baten deribatu partzial bat, azkar esanda, aldagai bakar batekiko deribatua da, hau da, beste aldagaiak konstante mantenduz aldagai bateko deribazioa egitea da.^[1] 

Deribatu partzialak era interesgarrietan konbina daitezke deribatuaren adierazpen konplexuagoak sortzeko. Kalkulu bektorialan, ${\displaystyle \nabla }$ ikurraren bidez gradientea edota dibergentzia definitzen dira, deribatu partzialetan oinarrituz. Deribatu partzialen matrize bat, matrize jakobiarra, edozein dimentsioko bi espazioren arteko funtzio baten deribatua irudikatzeko erabilgarria da. Hortaz, deribatua transformazio lineal baten gisa uler daiteke, funtzioaren eremuaren barruan puntu batetik bestera doana.

Deribatu partzialak dituzten ekuazio diferentzialei ekuazio diferentzial partzial edo EDP deritze. Ekuazio horiek, orokorrean, ekuazio diferentzial arruntak baino zailagoak dira ebazten, arruntak aldagai bakar batekiko deribatuak besterik ez baitituzte. ^[1]

Integrazio aniztuna

Integral aniztunak edozein aldagai kopururen funtzioetara zabaltzen du integral kontzeptua. Integral bikoitzak eta hirukoitzak planoko eta espazioko eskualdeen azalerak eta bolumenak kalkulatzeko erabil daitezke. Fubiniren teoremak integral anizkoitzak integral errepikatutzat edo iteratutzat har daitekeela bermatzen du, baldin eta integratzailea integrazioaren eremu osoan jarraitua bada.^[1] 

Gainazal-integrala eta lerro-integralak tolestura kurbatuak integratzeko erabiltzen dira, hala nola gainazalak tridimentsionalak eta kurbak.

Hainbat dimentsiotarako kalkuluaren oinarrizko teorema

Kalkuluaren oinarrizko teoremak deribatuaren eta integralaren arteko lotura ezartzen du aldagai bakarreko kalkuluan. Aldagai anitzeko kalkuluan, ordez, deribatuaren eta integralaren arteko lotura kalkulu bektorialaren teorema integralek irudikatzen dute:^[1]

• Gradientearen teorema
• Stokesen teorema
• Dibergentzia teorema
• Greenen teorema

Aldagai anitzeko kalkuluaren azterketa aurreratuago eta sakonagoa egiten bada, lau teorema horiek teorema orokorrago baten kasu bereziak direla, hain zuzen ere, Stokesen teorema orokorraren kasu bereziak. Teorema hau forma diferentzialen integrazioari buruzkoa da.^[2]

Aplikazioak eta erabilerak

Aldagai anitzeko kalkuluak ematen dizkigun teknikak mundu materialean interesgarriak diren objektu asko aztertzeko erabil daitezke. Bereziki,

		Funtzio-motak	Teknika aplikagarriak
Kurbak		${\displaystyle f:\mathbb {R} \to \mathbb {R} ^{n}}$, ${\displaystyle n>1}$ izanda	Kurben luzera, lerro-integralak eta kurbadura.
Azalera tridimentsionalak		${\displaystyle f:\mathbb {R} ^{2}\to \mathbb {R} ^{n}}$,${\displaystyle n>2}$ izanda	Gainazal tridimentsionalen azalerak, azalera-integralak, gainazalen bidezko fluxua eta kurbadura.
Eremu eskalarrak		${\displaystyle f:\mathbb {R} ^{n}\to \mathbb {R} }$	Maximoak eta minimoak, Lagrangeren biderkatzaileak, norabide-deribatuak, maila-multzoak...
Bektore-eremuak		${\displaystyle f:\mathbb {R} ^{m}\to \mathbb {R} ^{n}}$	Kalkulu bektorialeko edozein eragiketa, gradientea, dibergentzia eta kizkurra barne.

Aldagai anitzeko kalkulua askatasun-gradu anitz dituzten sistema deterministikoak aztertzeko erabil daiteke. Gehienetan, askatasun gradu bakoitzari dagozkion aldagai independenteak erabiltzen dituzten funtzioak aukeratzen dira sistema horiek modelatzeko. Horregatik, aldagai anitzeko kalkuluak sistemaren dinamika deskribatzeko tresnak eskaintzen ditu.

Aldagai anitzeko kalkulua denbora jarraitua duten sistema dinamikoen kontrol optimoa bermatzeko da. Erregresio-analisian erabili ohi da, datu-multzo enpirikoren arteko erlazioetatik zenbatesteko formulak deribatzeko.

Kalkulu aldagaianiztuna zientziaren eta ingeniaritzaren, naturalak zein sozialak, eremu askotan erabiltzen da, portaera determinista duten dimentsio handiko sistemak modelatzea eta aztertzea ahalbidetzen baitu. Ekonomian, adibidez, kontsumitzailearen aukera ondasun barietate handi baten aurrean, baita ekoizlearen aukerak osagai askoren artean eta produktu askoren artean, aldagai asko hartzen diruzte kontuan, eta kalkulu aldagaianiztuna tresna ezinhobea da modeloak sortzeko datu horiek kontutan izanda.

Sistema ez-deterministak (estokastikoak) matematikaren beste adarrak erabiliz azter daitezke, hala nola kalkulu estokastikoa.

Erreferentziak

Ikus gainera

• Aldagai anitzeko analisia (estatistika)
• Kalkulu diferentzial

Kanpo estekak

• Datuak: Q2035437
• Multimedia: Multivariate calculus / Q2035437