Kubikzahl
Eine Kubikzahl (von lateinisch cubus, „Würfel“) ist eine Zahl, die entsteht, wenn man eine natürliche Zahl zweimal mit sich selbst multipliziert. Beispielsweise ist eine Kubikzahl. Die ersten Kubikzahlen sind
- 0, 1, 8, 27, 64, 125, 216, 343, 512, 729, 1000, … (Folge A000578 in OEIS)
Bei einigen Autoren ist die Null keine Kubikzahl, sodass die Zahlenfolge erst mit der Eins beginnt.
Die Bezeichnung Kubikzahl leitet sich von der geometrischen Figur des Würfels her. Die Anzahl der Steine, die man zum Bauen eines Würfels benötigt, entspricht immer einer Kubikzahl. So lässt sich beispielsweise ein Würfel mit der Seitenlänge 3 mit Hilfe von 27 Steinen legen.
Aufgrund dieser Verwandtschaft mit einer geometrischen Figur zählen die Kubikzahlen zu den figurierten Zahlen, zu denen auch die Quadratzahlen und Tetraederzahlen gehören.
Eigenschaften
- Aus den aufeinanderfolgenden Blöcken von einer, zwei, drei, vier, fünf, … ungeraden natürlichen Zahlen in aufsteigender Reihenfolge lassen sich durch Summation die Kubikzahlen erzeugen:
- Ausgehend von der Folge der zentrierten Sechseckszahlen 1, 7, 19, 37, 61, 91, 127, 169, 217, 271, … erhält man die -te Kubikzahl als Summe der ersten Folgenglieder:
- Die Summe der ersten Kubikzahlen ist gleich dem Quadrat der -ten Dreieckszahl:
- Jede natürliche Zahl kann als Summe von höchstens neun Kubikzahlen dargestellt werden (Lösung des Waringschen Problems für den Exponenten 3). Dass 9 Summanden notwendig sein können, zeigt die Zahl 23. Diese hat die Darstellung
,
aber offensichtlich keine mit weniger kubischen Summanden. - Jede Kubikzahl lässt sich als Summe der ungeraden Zahlen zwischen zwei aufeinanderfolgenden doppelten Dreieckszahlen sowie als Differenz der Quadrate zweier sukzessiver Dreieckszahlen darstellen:
- Die Summe zweier beliebiger Kubikzahlen kann selbst nie eine Kubikzahl sein. Anders formuliert heißt dies, dass die Gleichung
keine Lösung mit natürlichen Zahlen besitzt. Dieser Spezialfall der Fermatschen Vermutung wurde 1753 von Leonhard Euler bewiesen. Lässt man mehr als zwei Summanden zu, kann es vorkommen, dass eine Kubikzahl als Summe von Kuben darstellbar ist, wie das folgende Beispiel (sogar mit drei direkt aufeinanderfolgenden Kubikzahlen) zeigt:
. - Wenn man von der Folge der Kubikzahlen den Modulo 9 nimmt, erhält man die periodische Folge (Folge A167176 in OEIS). Dies ergibt sich aus . Hieraus schließt sich ebenfalls, dass eine Zahl, die als Summe von drei Kubikzahlen darstellbar ist, niemals kongruent zu 4 oder 5 mod 9 sein kann.
Summe der Kehrwerte
Die Summe der Kehrwerte aller Kubikzahlen wird Apéry-Konstante genannt. Sie entspricht dem Wert der riemannschen -Funktion an der Stelle 3.
Erzeugende Funktion
Jeder Folge ganzer (oder reeller) Zahlen kann man eine formale Potenzreihe zuordnen, die sogenannte erzeugende Funktion . In diesem Kontext ist es allerdings üblich, die Folge der Kubikzahlen mit 0 beginnen zu lassen, also die Folge zu betrachten. Die erzeugende Funktion der Kubikzahlen ist dann
Geometrische Generierung
In der Kubikzahl ist die Basis eine reelle Zahl und der Exponent eine positive ganze Zahl. Aus diesem Grund ist der Potenzwert von auf einer Zahlengeraden als Konstruktion mit Zirkel und Lineal darstellbar.
Es ist zu unterscheiden, ob die Basis größer oder kleiner als die Zahl ist. Im Folgenden werden beide Möglichkeiten beschrieben.
Vorgehensweise für Basis > 1
- Ziehe auf der Zahlengeraden einen Kreisbogen um mit der Basis als Radius, bis er die Zahlengerade in schneidet.
- Bestimme den Abstand mit der Länge zum Punkt und errichte eine Senkrechte zur Zahlengeraden im Punkt , bis sie den Kreisbogen in schneidet.
- Verlängere die Basis mit einer Halbgeraden und errichte eine Senkrechte zur Zahlengeraden im Punkt , bis sie die Halbgerade in schneidet.
- Abschließend schneidet eine Senkrechte zur Strecke im Punkt die Zahlengerade in der Kubikzahl
-
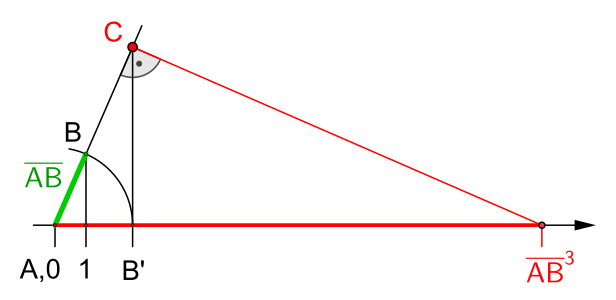 Konstruktion der Kubikzahl mit Basis
Konstruktion der Kubikzahl mit Basis -
 Konstruktion der Kubikzahl mit Basis
Konstruktion der Kubikzahl mit Basis
Vorgehensweise für Basis < 1
- Bestimme auf der Zahlengeraden die Basis als Strecke .
- Ziehe auf der Zahlengeraden einen Halbkreis um mit Radius , er schneidet die Zahlengerade in .
- Bestimme auf der Zahlengeraden ab die Strecke mit der Länge und ziehe einen Kreisbogen um mit Radius bis er den Halbkreis in schneidet.
- Fälle das Lot von auf mit Fußpunkt und verbinde den Punkt mit .
- Fälle das Lot von auf mit Fußpunkt .
- Der abschließende Kreisbogen um mit Radius bis auf die Zahlengerade liefert die Kubikzahl .
Tastatur
Auf der deutschen PC-Tastatur liegt das ³-Zeichen als dritte Belegung auf der 3-Taste und kann mit Hilfe der Alt-Gr-Taste eingegeben werden. Oft kann man auch statt Alt Gr die beiden Tasten Strg und Alt verwenden. Bei einer Apple-Tastatur hingegen gibt es keine definierte Tastenkombination für das ³-Zeichen. Das ³-Zeichen ist mit der Codenummer 179 (hexadezimal B3) Bestandteil der Zeichenkodierung ISO 8859-1 (bzw. ISO 8859-15) und damit auch des Unicodeblock Lateinisch-1, Ergänzung.
Siehe auch
Weblinks
- Eric W. Weisstein: Cubic Number. In: MathWorld (englisch).























































